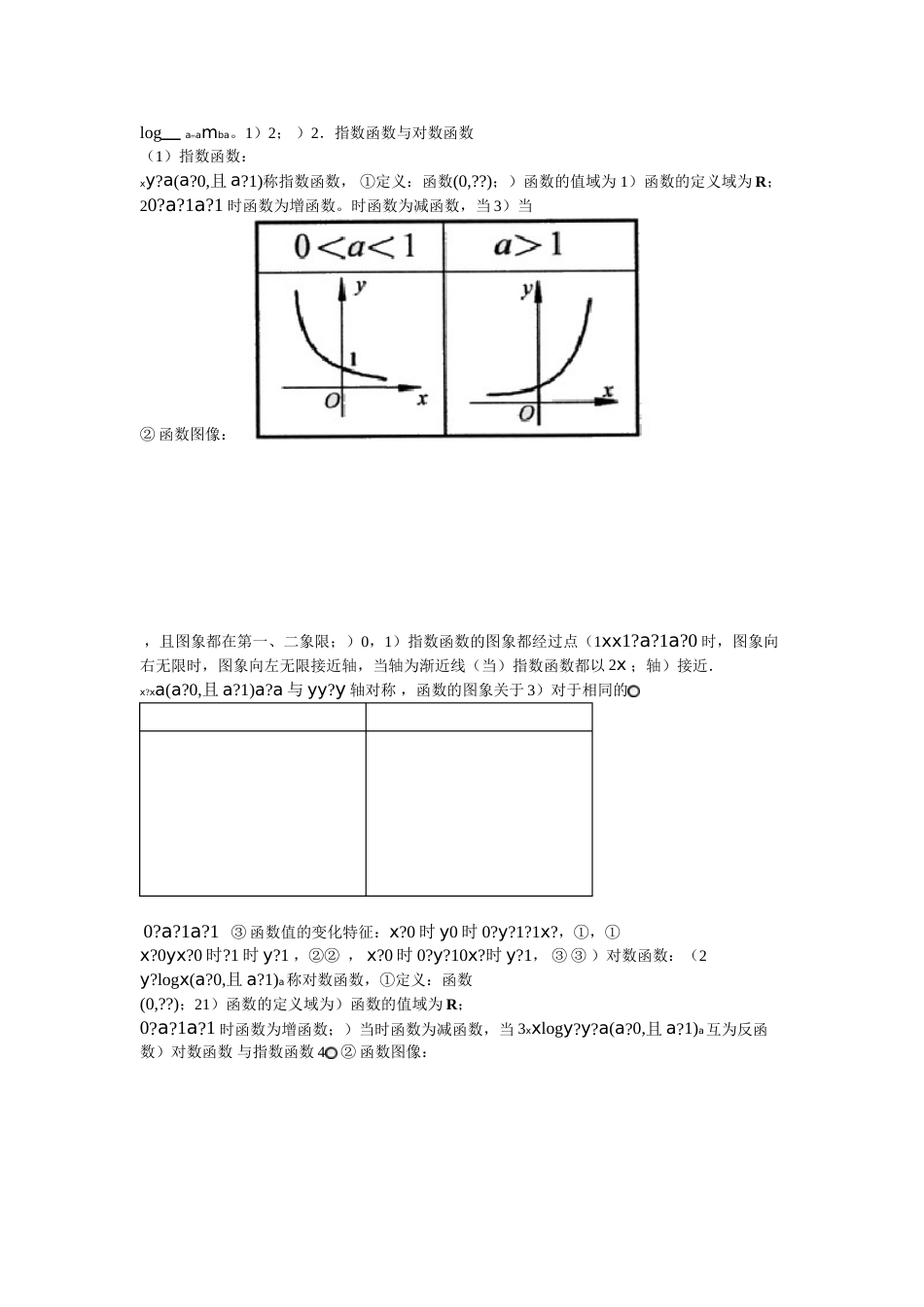
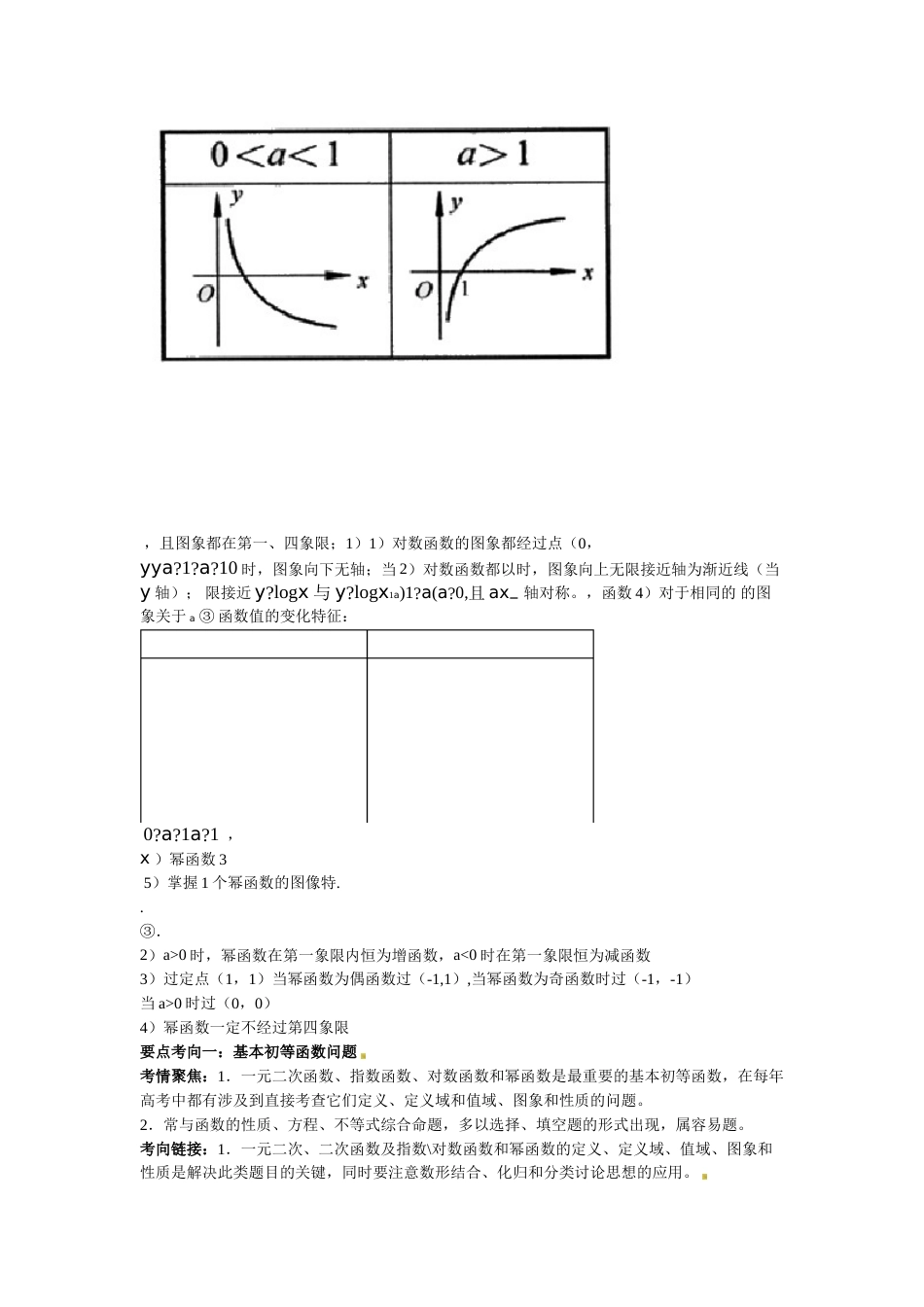
函数、基本初等函数1．指数函数14C的衰减，药物在人体内残留量的变化等），了（1）通过具体实例（如细胞的分裂，考古中所用的解指数函数模型的实际背景；（2）理解有理指数幂的含义，通过具体实例了解实数指数幂的意义，掌握幂的运算。（3）理解指数函数的概念和意义，能借助计算器或计算机画出具体指数函数的图象，探索并理解指数函数的单调性与特殊点；（4）在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型2．对数函数（1）理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；通过阅读材料，了解对数的发现历史以及对简化运算的作用；（2）通过具体实例，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型；能借助计算器或计算机画出具体对数函数的图象，探索并了解对数函数的单调性与特殊点；y?logxxy?aa与对数函数互为反函数（a＞0，3．知道指数函数a≠1）。4.幂函数（1）了解幂函数的概念1132xxx2x的图象，了解它们的变化情况,y=,y=y=x,,y=（2）结合函数,y=二．【命题走向】指数函数、对数函数、幂函数是三类常见的重要函数，在历年的高考题中都占据着重要的地位。从近几年的高考形势来看，对指数函数、对数函数、幂函数的考查，大多以基本函数的性质为依托，结合运算推理，能运用它们的性质解决具体问题。为此，我们要熟练掌握指数、对数运算法则，明确算理，能对常见的指数型函数、对数型函数进行变形处理。预测2010年对本节的考察是：1．题型有两个选择题和一个解答题；2．题目形式多以指数函数、对数函数、幂函数为载体的复合函数来考察函数的性质。同时它们与其它知识点交汇命题，则难度会加大【要点精讲】三．1．指数与对数运算（1）根式的概念：?)1,且n?Na(n?nxnanax?称①定义：若一个数的次方等于则这个数称，，的则次方根。即若?)?N1且nn?na次方根，的nann的a1）当次方根记作为奇数时，；n)?a(a?0nnana记作没有次方根，而正数有两个次方根且互为相反数，2）当为偶数时，负数nna?(a)nna?an为奇数时，2②性质：1）当；）；)?0a(a?n?|a?|a?)0?a(a?n?为偶数时，。3）当．幂的有关概念2）（0n)?0?a1(aa???a(n?a?a?*）；2①规定：1）；N个n1mp??ap(?mnm?0,a?a(a)?1nnp?na*）、N），且43Qs?rsrr,?0a?a?a(a?s；1）Q）②性质：、s?srrr,?0?a(a(a)?s）；Q）、2rrr?,rb?0?b(a?0,)(a?b?a。）3）Q?s均适用。R（注）上述性质对r、．对数的概念（3）)1a??0,且aa(baN?ab的对数，记为底①定义：如果的b次幂等于N，就是称以N，那么数,blogN?aa称真数称对数的底，N作其中NlogNlg10记作101）以为底的对数称常用对数，；logN)2?.71828?ee(lnNe2）以无理数；为底的对数称自然对数，，记作②基本性质：log1?0a；）1）真数N为正数（负数和零无对数）；2loga?1logN?Naaa。；4）对数恒等式：3）a?0,a?0,M?0,N?0,则③运算性质：如果log(MN)?logM?logNaaa；）1M?logM?loglogNaaaN；2）n?nlogMMlog(n?aaR3））logNm(a?0,a?0,m?0,m?1logN?,N?0),aloga④换底公式：mnnlogblogb?1loga?b?logamamba。1）2；）2．指数函数与对数函数（1）指数函数：xy?a(a?0,且a?1)称指数函数，①定义：函数(0,??)；）函数的值域为1）函数的定义域为R；20?a?1a?1时函数为增函数。时函数为减函数，当3）当②函数图像：，且图象都在第一、二象限；）0，1）指数函数的图象都经过点（1xx1?a?1a?0时，图象向右无限时，图象向左无限接近轴，当轴为渐近线（当）指数函数都以2x；轴）接近．x?xa(a?0,且a?1)a?a与yy?y轴对称，函数的图象关于3）对于相同的0?a?1a?1③函数值的变化特征：x?0时y0时0?y?1?1x?，①，①x?0yx?0时?1时y?1，②②，x?0时0?y?10x?时y?1，③③）对数函数：（2y?logx(a?0,且a?1)a称对数函数，①定义：函数(0,??)；21）函数的定义域为）函数的值域为R；0?a?1a?1时函数为增函数；）当时函数为减函数，当3xxlogy?y?a(a?0,且a?1)a互为反函数）对数函数与指数函数4②函数图像：，且图象都在第一、四象限；1）1）对数函数的图象都经过点（0，yya?1?a?10时，图象向下无轴；当2）对数函数都以时，图象向上无限接近轴为...