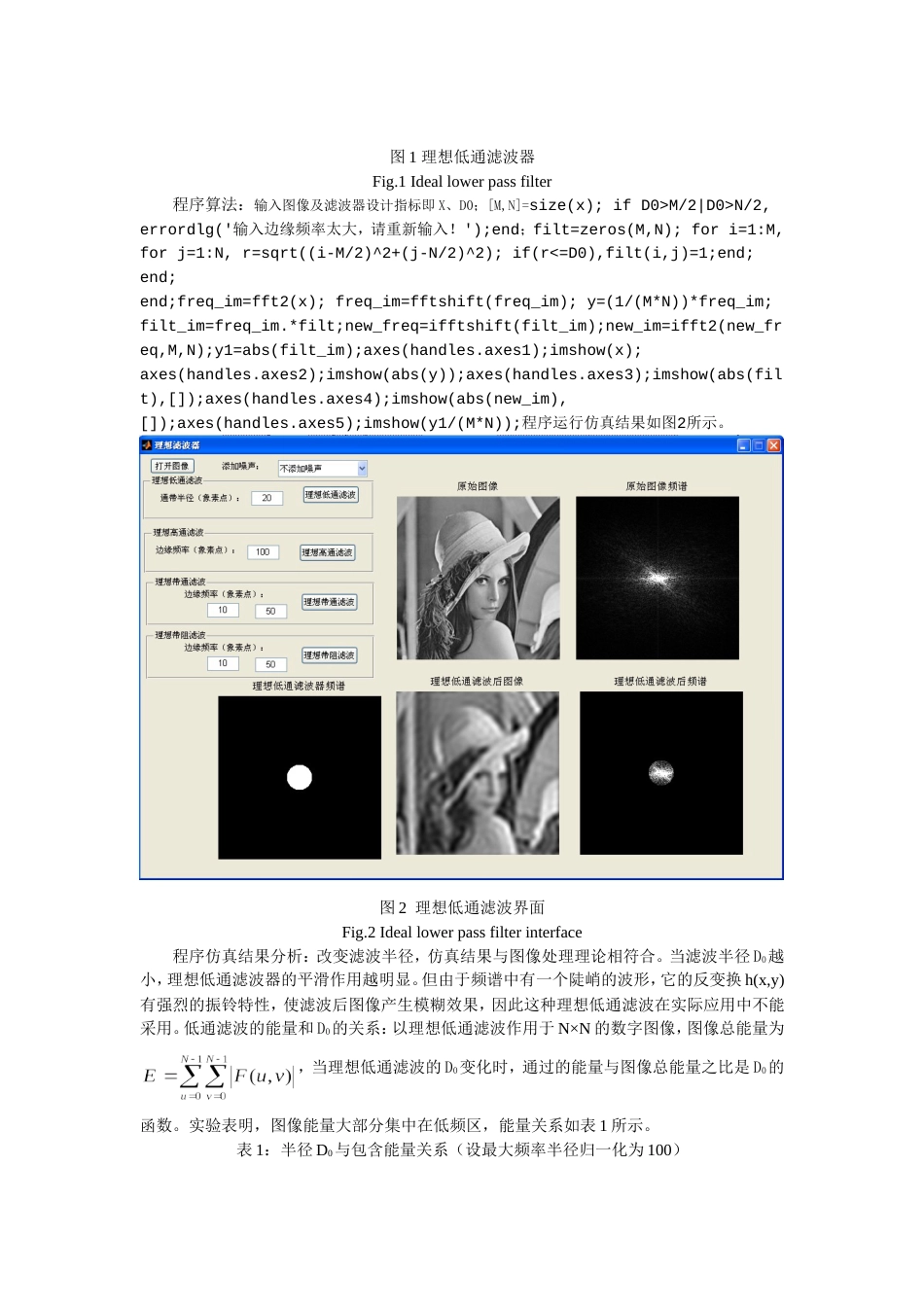
基于Matlab的数字图像二维滤波软件设计陈金西(厦门理工学院电子与电气工程系,福建厦门361024)[摘要]本设计采用Matlab程序，设计数字图像二维滤波平台，用户可任意给定滤波参数及图像，即可观察滤波器特征图像、图像的滤波效果，并可根据需要存储结果。这种可视化处理过程，形象直观便于理解和学习图像处理过程和二维滤波器系统特征。本设计开发目的是给数字图像滤波处理的学习与分析研究提供一个软件平台。[关键词]二维滤波器；数字图像；MatLab；仿真；多媒体教学[中图分类号]TN911.6；TP31[文献标识码]AThedesignofthe2-dimensionfilterfordigitalimagebasedonMatlabCHENJin-xi(ElectronicEngineeringDepartmentunderXiamenUniversityofTechnology,Xiamen361024,China)Abstract:ThisdesignuseMatlablanguagetobuildaemluatingplatformoffilterfordigitalimage.Itmaymodifyaormoreparameterstostudy2-dimensionfiltersystemcharacter.Itactsasatoolforanalysisandstudyoffiltersystemdesignandalsoasassistantwayofmultimediateachingforlessons,i.e.‘digitalimageprocessing’,etc.Keywords:2-dimensionfilter;digitalimage;matlab;simulation;multimediateaching0前言滤波器的功能是允许某一部分频率的信号顺利通过，而另外一部分频率的信号则受到较大的抑制。滤波器中，把信号能够通过的频率范围，称为通频带或通带；反之，信号受到很大衰减或完全被抑制的频率范围称为阻带；通带和阻带之间的分界频率称为截止频率。理想滤波器在通带内的电压增益为常数，在阻带内的电压增益为零。实际滤波器的通带和阻带之间存在一定频率范围，称此频率范围为过渡带；在通带内的电压增益不是常数而是具有一定的波动范围，称此波动范围为通带波动；在阻带内的电压增益不是零而是具有一定的波动范围，称此范围为阻带波动。由于数字图像滤波器是二维滤波器，数学模型复杂，不易理解，本设计采用Matlab语言，设计数字图像二维滤波器平台，用户可任意给定滤波参数，即可观察二维滤波器的系统特征图像、图像的滤波效果，并可根据需要存储结果。这种可视化处理过程，形象直观便于理解图像处理过程和二维滤波器系统特征，可提高教学效率。本设计已应用于教学实践中，得到学生普遍好评。1系统设计与仿真1.1理想低通滤波设计理想低通滤波器是指小于D0的频率可以完全不受影响地通过滤波器，而大于D0的频率则完全通不过，如图1所示。理想低通滤波函数：，其中D0为截断频率，是从点(u,v)到频率平面原点的距离。图1理想低通滤波器Fig.1Ideallowerpassfilter程序算法：输入图像及滤波器设计指标即X、D0；[M,N]=size(x);ifD0>M/2|D0>N/2,errordlg('输入边缘频率太大，请重新输入！');end；filt=zeros(M,N);fori=1:M,forj=1:N,r=sqrt((i-M/2)^2+(j-N/2)^2);if(r<=D0),filt(i,j)=1;end;end;end;freq_im=fft2(x);freq_im=fftshift(freq_im);y=(1/(M*N))*freq_im;filt_im=freq_im.*filt;new_freq=ifftshift(filt_im);new_im=ifft2(new_freq,M,N);y1=abs(filt_im);axes(handles.axes1);imshow(x);axes(handles.axes2);imshow(abs(y));axes(handles.axes3);imshow(abs(filt),[]);axes(handles.axes4);imshow(abs(new_im),[]);axes(handles.axes5);imshow(y1/(M*N));程序运行仿真结果如图2所示。图2理想低通滤波界面Fig.2Ideallowerpassfilterinterface程序仿真结果分析：改变滤波半径，仿真结果与图像处理理论相符合。当滤波半径D0越小，理想低通滤波器的平滑作用越明显。但由于频谱中有一个陡峭的波形，它的反变换h(x,y)有强烈的振铃特性，使滤波后图像产生模糊效果，因此这种理想低通滤波在实际应用中不能采用。低通滤波的能量和D0的关系：以理想低通滤波作用于N×N的数字图像，图像总能量为，当理想低通滤波的D0变化时，通过的能量与图像总能量之比是D0的函数。实验表明，图像能量大部分集中在低频区，能量关系如表1所示。表1：半径D0与包含能量关系（设最大频率半径归一化为100）半径D0包含总能量(%)半径D0包含总能量(%)590.03699.01196.05399.52298.09899.91.2理想高通滤波设计理想高通滤波器是指大于D0的频率...