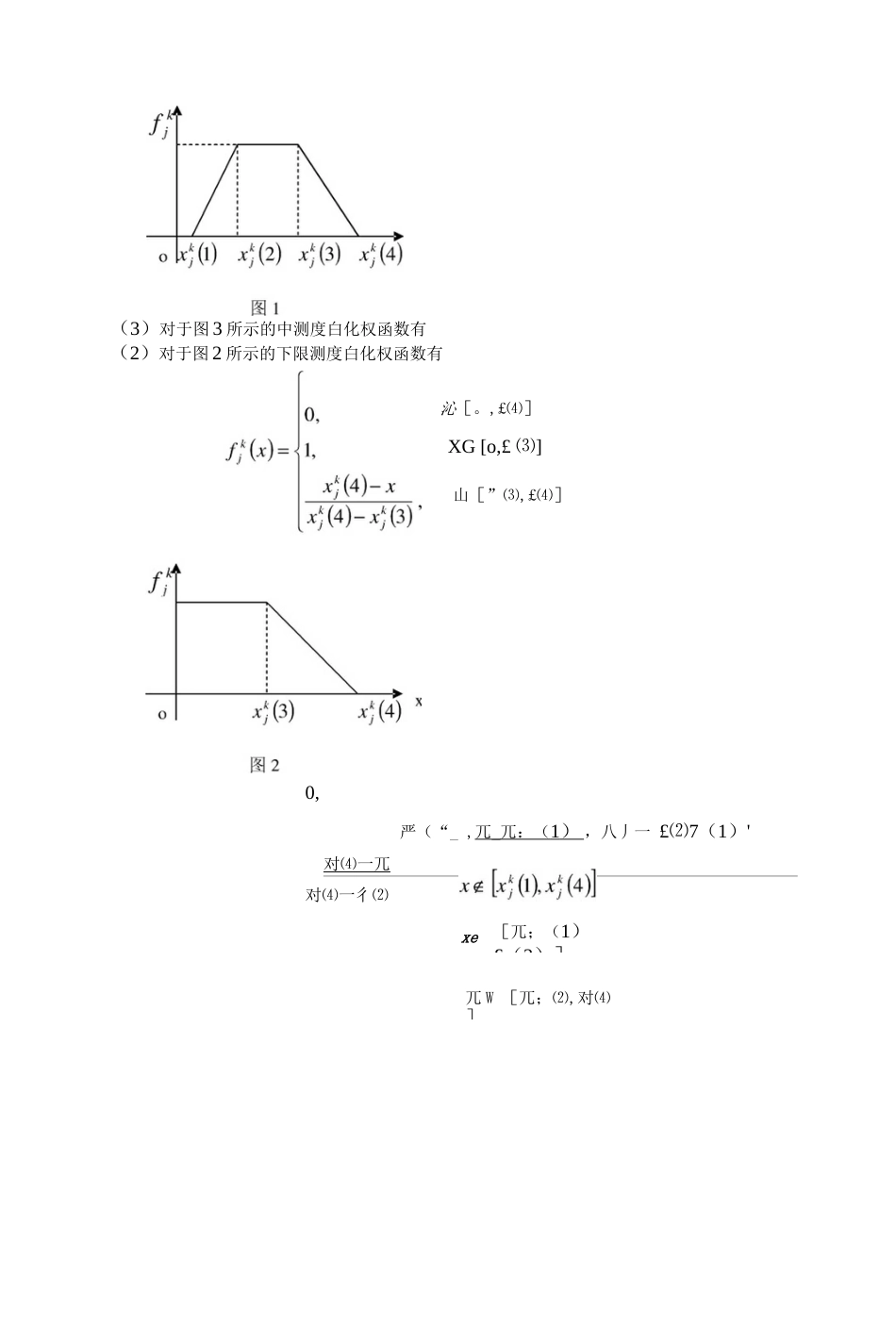
灰色聚类方法综述杨雅捷(西安理工大学理学院，陕西西安710054)摘要：灰色聚类是根拯灰色关联矩阵或灰数的白化权函数将一些观测指标或观测对象划分成若T个可定义类别的方法。一个聚类可以看成是属于同一类的观测对象的集合。灰色聚类分为灰色关联聚类和灰色白化权函数聚类。灰色关联聚类主要用于同类因素的归并，以使复杂系统简化。灰色白化权函数聚类主要用于检查观测对象是否属于事先设定的不同类别，以便区别对待。它的应用十分广泛，本文具体举例说明灰色聚类方法的应用情况，以及对其进行改进提出一些建议。关键词：灰色系统理论；灰色聚类；应用及改进措施文献表示码：A中图分类号：N941.5ThesummarizeofgreyclusteringmethodYANG-Yajie(Xi'anUniversityofTechnologySchoolofScienceShaanxiXi'an710054)Abstract:Greyclusteringfunctiondividedobservationtargetsorobservationobjectsintoanumberofmethodthatcanbedefined,whichisbasedongreyrelationalmatrixorgreywhiteningweight.Aclustercanbeseenasasetofthesameobservationobjects.Greyclusterisdiviedintogreyrelationalclusteringandgreywhiteningweightfunctionclustering・Greyrelationalclusterismainlyusedformergingofsimilarfactors,tomakecomplexsystemseasier.Greywhiteningweightfunctionclusteringismainlyusedforcheckingwhethertheobservationofdifferentcategoriesofobiectsaresetinadvancesothatitcanbetreateddifferently.Itapplicationiswidelyused.Thisarticleillustratestheapplicationofgreyclusteringmethod,Aswellastoimproveit.Keywords:Greysystemtheory,Greyclustering,Applicationandimprovementmeasures1前言灰色系统理论是邓聚龙教授80年代初提出的，在短短几十年间，得到了长足发展，目前，在我国已成功运用到了社会，经济，科教等各个方面，成为这些领域中进行预测，决策，分析和控制的有力工具⑴。它是以“部分信息已知，部分信息未知”的“小样木”、“贫信息”不确定性系统为研究对彖，着重研究“外延明确、内涵不明确”的对彖，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为的正确认识和评价。灰色系统分析包括灰色关联、灰色聚类和灰色统计评估。其中灰色聚类方法是发展较早并应用较广的一种方法(2'5,o灰色聚类可分为灰色关联聚类和灰色白化权函数聚类。灰色关联聚类主要于同类因素的归并，使复杂系统简单化，展于变量删减问题。灰色白化权函数聚类主要用于检查观测对象是否屈于事先设定的不同类别。灰色白化权函数聚类又包括灰色变权聚类和灰色定权聚类两种W灰色变权聚类适用于指标的意义、量纲皆相同的情形。当聚类指标的意义、量纲不同，且在数量上悬殊较大时，变权聚类可能导致某些指标参与聚类的作用十分微弱。解决这一问题有两种方法：一条途径是采用初值化算子或均值化算子将各个指标值化为无量纲数据，然后进行聚类。另一条途径是各聚类指标事先赋权，即为灰色定权聚类If2灰色聚类的基本概念灰色聚类法⑹(灰类白化权函数聚类法)是建立在灰数的白化函数牛成基础上的一种方法，它是将聚类对象(评价对彖)对不同聚类指标(评价指标)所拥有的白化值(实测值或分析数据)按N个灰类(评价等级)进行归纳整理，从而判断聚类对象属于哪一类的灰色统计法。2.1灰色关联聚类定义2.1.1设有〃个观测对象，每个对象观测加个特征数据，得到序列如下:X]=(兀](1),尢](2),…，兀](/?))X2=(X2(1),X2(2),---,X2(H))X”=(£(1)心(2),・.・,兀“(刃))对所有的/<计算出乙与勒的灰色关联度s•得上三角矩阵其中，=1J=1,2,…，加。称矩阵A为特征变量关联矩阵。取定临界值re[0,1],一般要求/*>0.5,当昭心j)时，则视£与X,为同类特征。定义2.1.2特征变量在临界值厂下的分类称为特征变量的r灰色关联聚类。厂可根据实际问题的需要确定，厂越接近于1,分类越细，每一组分中的变量相对的越少；厂越小，分类越粗，这时每一组分中的变量相对的越多。2.2灰色变权聚类命题2.2.1(1)对于图1所示的典型白化权函数，有0,x-X：⑴1,Xj⑷-X璟4)7⑶亦［兀；(1)，尢：⑷］"［彳⑴，兀;⑵］氏k...