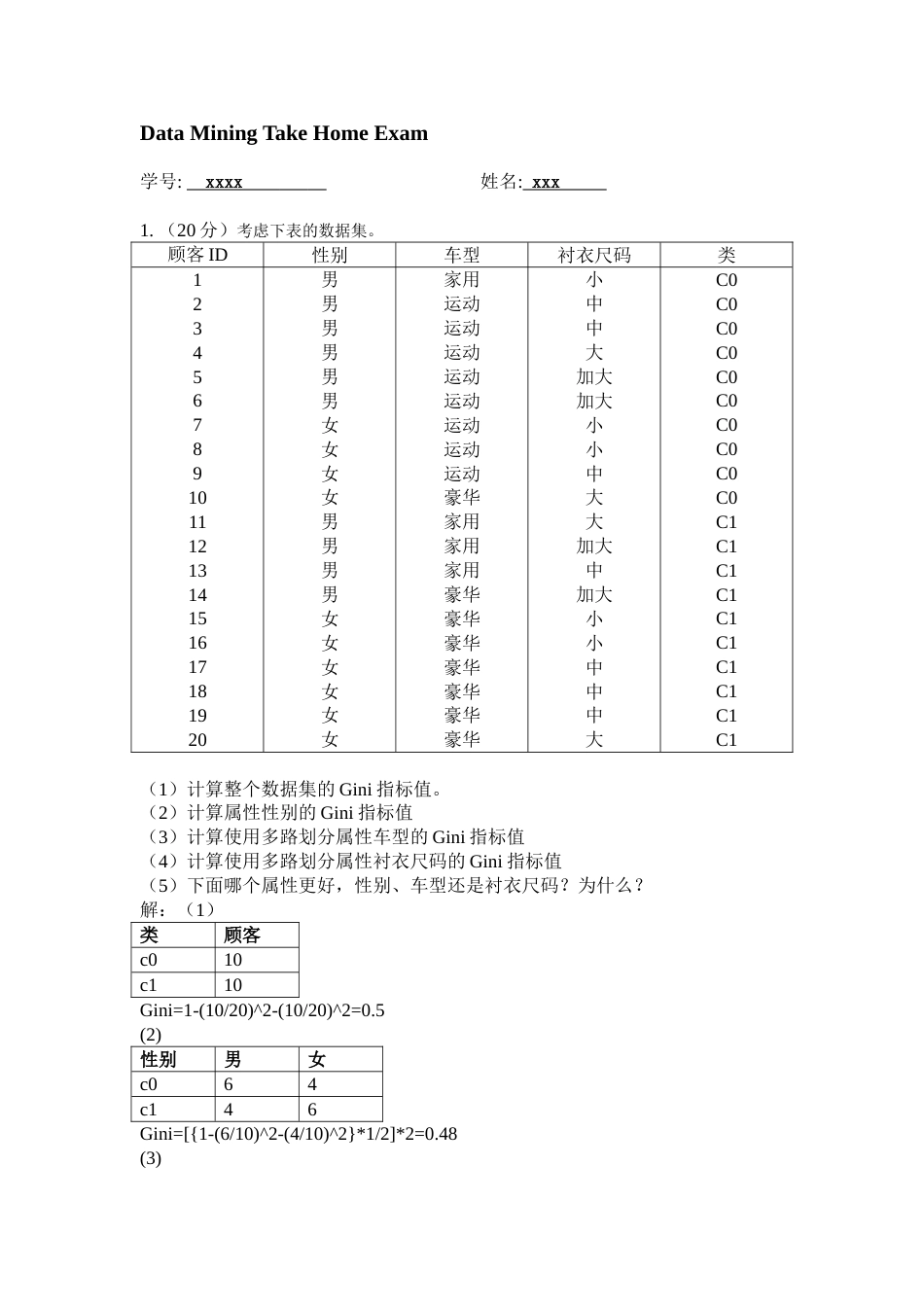
DataMiningTakeHomeExam学号:xxxx姓名:xxx1.（20分）考虑下表的数据集。顾客ID性别车型衬衣尺码类1234567891011121314151617181920男男男男男男女女女女男男男男女女女女女女家用运动运动运动运动运动运动运动运动豪华家用家用家用豪华豪华豪华豪华豪华豪华豪华小中中大加大加大小小中大大加大中加大小小中中中大C0C0C0C0C0C0C0C0C0C0C1C1C1C1C1C1C1C1C1C1（1）计算整个数据集的Gini指标值。（2）计算属性性别的Gini指标值（3）计算使用多路划分属性车型的Gini指标值（4）计算使用多路划分属性衬衣尺码的Gini指标值（5）下面哪个属性更好，性别、车型还是衬衣尺码？为什么？解：（1）类顾客c010c110Gini=1-(10/20)^2-(10/20)^2=0.5(2)性别男女c064c146Gini=[{1-(6/10)^2-(4/10)^2}*1/2]*2=0.48(3)车型家用运动豪华c0181c1307Gini={1-(1/4)^2-(3/4)^2}*4/20+{1-(8/8)^2-(0/8)^2}*8/20+{1-(1/8)^2-(7/8)^2}*8/20=26/160=0.1625(4)尺码小中大加大c03322c12422Gini={1-(3/5)^2-(2/5)^2}*5/20+{1-(3/7)^2-(4/7)^2}*7/20+[{1-(2/4)^2-(2/4)^2}*4/20]*2=8/25+6/35=0.4914(5)比较上面各属性的Gini值大小可知，车型划分Gini值0.1625最小，即使用车型属性更好。2.（20分）考虑下表中的购物篮事务数据集。顾客ID事务ID购买项1122334455001002400120031001500220029004000330038{a,d,e}{a,b,c,e}{a,b,d,e}{a,c,d,e}{b,c,e}{b,d,e}{c,d}{a,b,c}{a,d,e}{a,b,e}(1)将每个事务ID视为一个购物篮，计算项集{e}，{b,d}和{b,d,e}的支持度。（2）使用（1）的计算结果，计算关联规则{b,d}→{e}和{e}→{b,d}的置信度。（3）将每个顾客ID作为一个购物篮，重复（1）。应当将每个项看作一个二元变量（如果一个项在顾客的购买事务中至少出现一次，则为1，否则，为0）。（4）使用（3）的计算结果，计算关联规则{b,d}→{e}和{e}→{b,d}的置信度。答：（1）由上表计数可得{ｅ}的支持度为8/10=0.8；{ｂ，ｄ}的支持度为2/10=0.2；｛b,d,e｝的支持度为2/10=0.2。（2）c[{b,d}→{e}]=2/8=0.25;c[{e}→{b,d}]=8/2=4。（3）同理可得：{e}的支持度为4/5=0.8，{b,d}的支持度为5/5=1，{b,d,e}的支持度为4/5=0.8。（4）c[{b,d}→{e}]=5/4=1.25，c[{e}→{b,d}]=4/5=0.8。3.（20分）以下是多元回归分析的部分R输出结果。>ls1=lm(y~x1+x2)>anova(ls1)DfSumSqMeanSqFvaluePr(>F)x1110021.210021.262.0380.0001007***x214030.94030.924.9540.0015735**Residuals71130.7161.5>ls2<-lm(y~x2+x1)>anova(ls2)DfSumSqMeanSqFvaluePr(>F)x213363.43363.420.8220.002595**x1110688.710688.766.1708.193e-05***Residuals71130.7161.5（1）用F检验来检验以下假设(α=0.05)H0:β1=0Ha:β1≠0计算检验统计量；是否拒绝零假设，为什么？（2）用F检验来检验以下假设(α=0.05)H0:β2=0Ha:β2≠0计算检验统计量；是否拒绝零假设，为什么？（3）用F检验来检验以下假设(α=0.05)H0:β1=β2=0Ha:β1和β2并不都等于零计算检验统计量；是否拒绝零假设，为什么？解：（1）根据第一个输出结果F=62.083>F（2，7）=4.74，p<0.05，所以可以拒绝原假设，即得到不等于0。（2）同理，在α=0.05的条件下，F=20.822>F(2,7)=4.74，p<0.05，即拒绝原假设，得到不等于0。（3）F={（10021.2+4030.9）/2}/（1130.7/7）=43.4973>F=(2,7)=4.74,即拒绝原假设，得到和并不都等于0。4.（20分）考虑下面20个观测值：[1]-20.00-0.516-1.249-0.51025.000[6]-0.561-0.928-0.0230.7140.374[11]-0.3770.8300.8380.874-1.306[16]1.1381.087-1.4892.5240.713（1）用3*S标准来检测该数据中是否存在异常值。（2）用1.5*IQR标准来检测该数据中是否存在异常值。要求提供均值、标准差、IQR值和所用的区间，以及你判断的依据。解：数据放入R运行得>hhh=c(-20.00,-0.516,-1.249,-0.510,25.000,++-0.561,-0.928,-0.023,0.714,0.374,++-0.377,0.830,0.838,0.874,-1.306,++1.138,1.087,-1.489,2.524,0.713)>mean(hhh)[1]0.35665>sqrt(var(hhh))[1]7.405346>jjj<-(hhh-mean(hhh))/sqrt(var(hhh))>which(abs(jjj)>=3)[1]5>Q1=quantile(hhh,0.25)>Q3=quantile(hhh,0.75)>IQR=Q3-Q1>Q125%-0.6527...