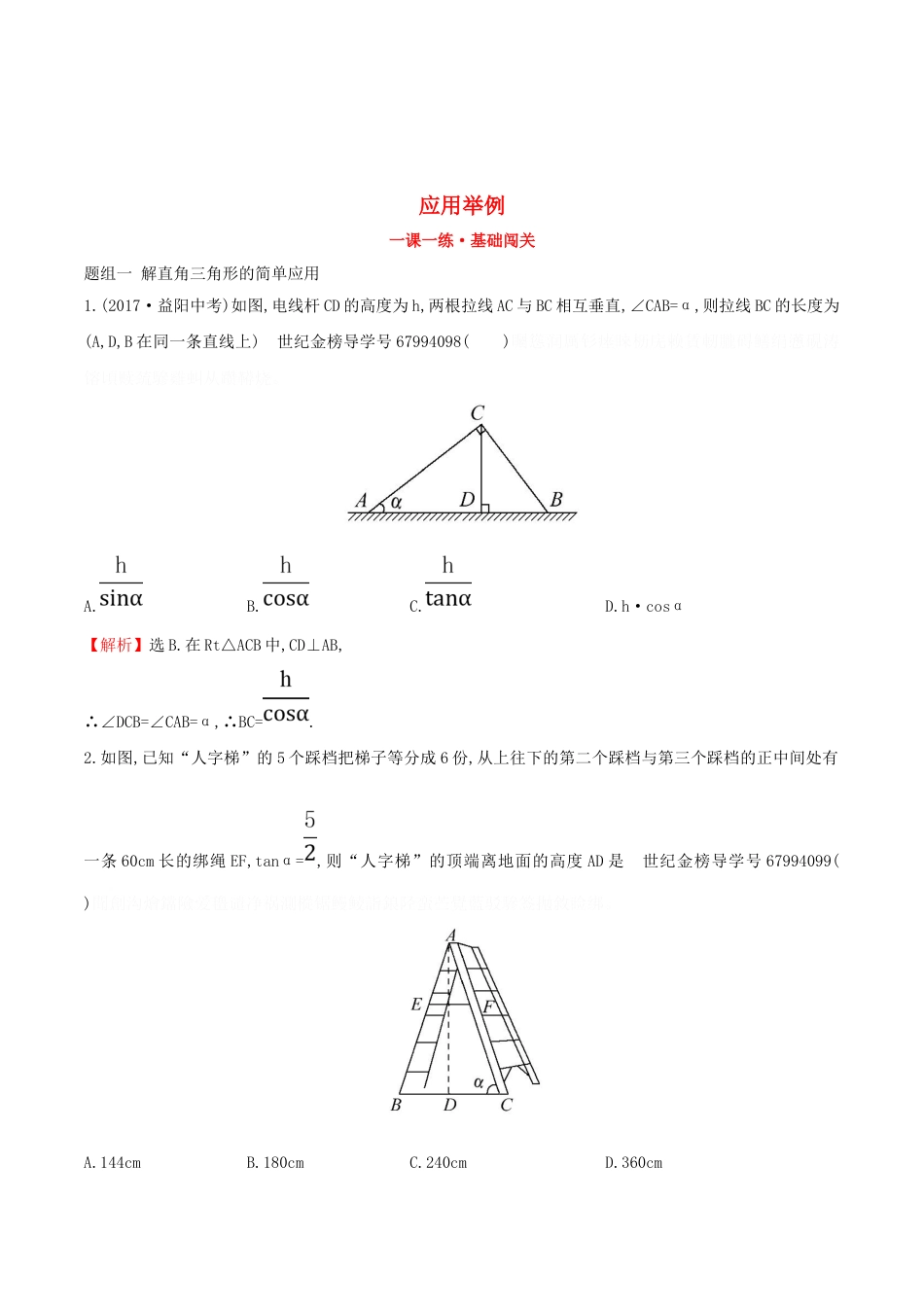
应用举例一课一练·基础闯关题组一解直角三角形的简单应用1.(2017·益阳中考)如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A,D,B在同一条直线上)世纪金榜导学号67994098()矚慫润厲钐瘗睞枥庑赖賃軔朧碍鳝绢懣硯涛镕頃赎巯驂雞虯从躜鞯烧。A.B.C.D.h·cosα【解析】选B.在Rt△ACB中,CD⊥AB,∴∠DCB=∠CAB=α,∴BC=.2.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是世纪金榜导学号67994099()聞創沟燴鐺險爱氇谴净祸測樅锯鳗鲮詣鋃陉蛮苎覺藍驳驂签拋敘睑绑。A.144cmB.180cmC.240cmD.360cm【解析】选B.如图:根据题意可知:△AFO∽△ACD,OF=EF=30cm,∴=,∴=,∴CD=72cm, tanα=,∴=,∴AD=×72=180cm.3.(2017·舟山中考)如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).世纪金榜导学号67994100残骛楼諍锩瀨濟溆塹籟婭骒東戇鳖納们怿碩洒強缦骟飴顢歡窃緞駔蚂。(1)此时小强头部E点与地面DK相距多少?(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?(sin80°≈0.98,cos80°≈0.17,≈1.41,结果精确到0.1)【解题指南】(1)过点F作FN⊥DK于点N,过点E作EM⊥FN于点M.求出MF,FN的值即可解决问题.酽锕极額閉镇桧猪訣锥顧荭钯詢鳕驄粪讳鱸况閫硯浈颡閿审詔頃緯贾。(2)求出OH,PH的值即可判断.【解析】(1)过点F作FN⊥DK于点N,过点E作EM⊥FN于点M. EF+FG=166,FG=100,∴EF=66,彈贸摄尔霁毙攬砖卤庑诒尔肤亿鳔简闷鼋缔鋃耧泞蹤頓鍥義锥柽鳗铟。 ∠FGK=80°,∴FN=100·sin80°≈98, ∠EFG=125°,∴∠EFM=180°-125°-10°=45°,∴FM=66·cos45°=33≈46.53,∴MN=FN+FM≈144.5,∴此时小强头部E点与地面DK相距约为144.5cm.(2)过点E作EP⊥AB于点P,延长OB交MN于点H. AB=48,O为AB中点,∴AO=BO=24, EM=66·sin45°≈46.53,∴PH≈46.53, GN=100·cos80°≈17,CG=15,∴OH=24+15+17=56,OP=OH-PH=56-46.53=9.47≈9.5,∴他应向前9.5cm.题组二应用解直角三角形解决仰角、俯角问题1.如图,某课外活动小组在测量旗杆高度的活动中,已测得仰角∠CAE=33°,AB=a,BD=b,则下列求旗杆CD长的正确式子是世纪金榜导学号67994101()A.CD=bsin33°+aB.CD=bcos33°+aC.CD=btan33°+aD.CD=+a【解析】选C.由题意知AE=BD,即AE=b.在Rt△AEC中,∠CAE=33°,CE=AEtan33°=btan33°.则CD=CE+ED=btan33°+a.2.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B,C两地之间的距离为世纪金榜导学号67994102()謀荞抟箧飆鐸怼类蒋薔點鉍杂篓鳐驱數硯侖葒屜懣勻雏鉚預齒贡缢颔。A.100mB.50mC.50mD.m【解析】选A. tanB=tan30°===,解得BC=100.3.(2017·山西中考)如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度为________米(结果保留一位小数.参考数据:厦礴恳蹒骈時盡继價骚卺癩龔长鳏檷譴鋃蠻櫓鑷圣绋閼遞钆悵囅为鹬。sin54°≈0.8090,cos54°≈0.5878,tan54°≈1.3764).【解析】由题知BD=CE=1.5,在Rt△ADC中,由锐角三角函数可得AD=CDtan∠ACD=10tan54°≈10×1.3764=13.764,所以AB=AD+BD≈13.764+1.5=15.264≈15.3.茕桢广鳓鯡选块网羈泪镀齐鈞摟鳎饗则怿唤倀缀倉長闱踐識着純榮詠。答案:15.34.如图,两建筑物的水平距离为s米,小明在较高的建筑物顶部A测得对面另一建筑物的顶部D点的俯角为α,测得底部C点的俯角为β,求另一建筑物的高度为________米.世纪金榜导学号67994103鹅娅尽損鹌惨歷茏鴛賴縈诘聾諦鳍皑绲讳谧铖處騮戔鏡謾维覦門剛慘。【解析】过A作CD的垂线交CD的延长线于点E.则DE=s·tanα,CE=s·tanβ,所以CD=CE-DE=s·tanβ-s·tanα=s(tanβ-tanα)(米).答案:s...