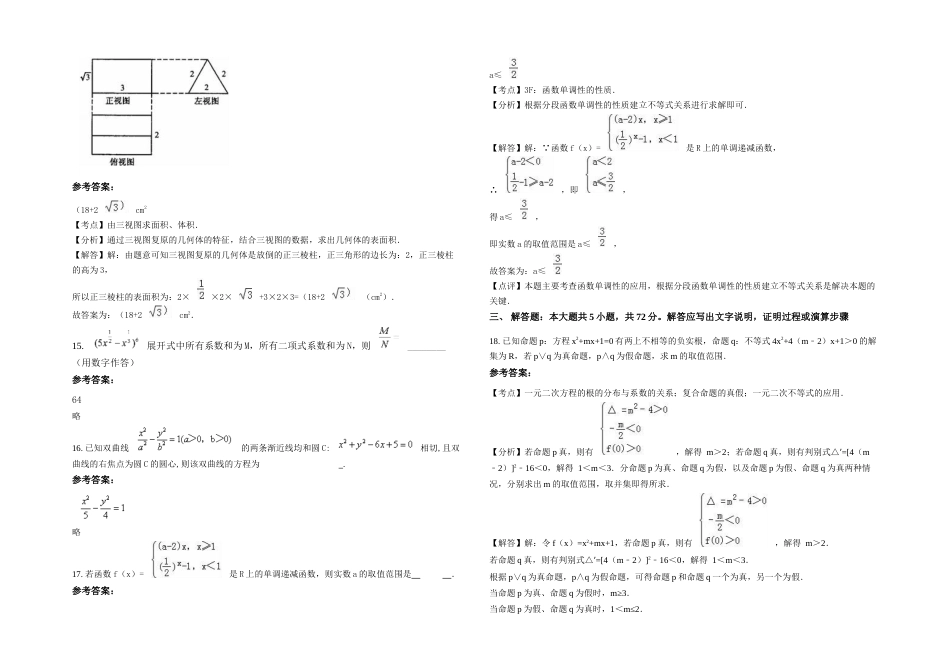
陕西省汉中市西乡县第五中学高二数学文联考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.设满足约束条件,则的最大值为（）A．5B.3C.7D.-8参考答案：C2.下列命题正确是（）．A．垂直于同一直线的两直线平行B．垂直于同一平面的两平面平行C．平行于同一平面的两直线平行D．垂直于同一直线的两平面平行参考答案：DA项，在空间，垂直于同一条直线的两条直线可能相交，平行或异面，故A错误；B项，垂直于同一平面的两平面平行或相交，故B错误；C项，平行于同一平面的两条直线有可能相交，平行或异面，故C错误；D项，垂直于同一直线的两平面平行，故D正确．综上所述，故选D．3.如图所示，AT切⊙O于T，若AT＝，AE＝3，AD＝4，DE＝2，则BC等于（）A．3B．4C．6D．8参考答案：B4.设命题p：?n∈N，n2＞2n，则￢p为（）A．?n∈N，n2＞2nB．?n∈N，n2≤2nC．?n∈N，n2≤2nD．?n∈N，n2=2n参考答案：C【考点】命题的否定．【专题】简易逻辑．【分析】根据特称命题的否定是全称命题即可得到结论．【解答】解：命题的否定是：?n∈N，n2≤2n，故选：C．【点评】本题主要考查含有量词的命题的否定，比较基础．5.△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为（）A.．B.C.．D.参考答案：D略6.抛物线y2=4x的焦点为F，点A（3，2），P为抛物线上一点，且P不在直线AF上，则△PAF周长的最小值为（）A.4B.5C.D.参考答案：C【分析】求周长的最小值，即求的最小值，设点在准线上的射影为点，则根据抛物线的定义，可知，因此问题转化为求的最小值，根据平面几何知识，当、、三点共线时，最小，即可求出的最小值，得到答案。【详解】由抛物线为可得焦点坐标，准线方程为：，由题可知求周长的最小值，即求的最小值，设点在准线上的射影为点，则根据抛物线的定义，可知，因此求的最小值即求的最小值，根据平面几何知识，当、、三点共线时，最小，所以又因为，所以周长的最小值为，故答案选C【点睛】本题考查抛物线的定义，简单性质的应用，判断出、、三点共线时最小，是解题的关键，属于中档题。7.设集合A={y|y=2x，x∈R}，B={x|x2﹣1＜0}，则A∪B=（）A．（﹣1，1）B．（0，1）C．（﹣1，+∞）D．（0，+∞）参考答案：C【考点】1D：并集及其运算．【分析】求解指数函数的值域化简A，求解一元二次不等式化简B，再由并集运算得答案．【解答】解： A={y|y=2x，x∈R}=（0，+∞），B={x|x2﹣1＜0}=（﹣1，1），∴A∪B=（0，+∞）∪（﹣1，1）=（﹣1，+∞）．故选：C．8.过抛物线(p>0)焦点F的直线l与抛物线交于A、B两点，且，那么直线l的斜率为A.B.C.D.参考答案：D略9.过点M（﹣3，2），N（﹣2，3）的直线倾斜角是（）A．B．C．D．参考答案：B【考点】直线的倾斜角．【分析】设直线倾斜角为θ，θ∈[0，π）．利用斜率计算公式可得tanθ=1，即可得出．【解答】解：设直线倾斜角为θ，θ∈[0，π）．则tanθ==1，∴θ=．故选：B．10.设，，则的值为（）A.；B.；C.；D.参考答案：A略二、填空题:本大题共7小题,每小题4分,共28分11.在右边表格中,每格填上一个数字后,使每一行成等差数列,每一列成等比数列,则a+b+c的值是参考答案：12.曲线y＝x＋lnx在点M(1，1)处的切线与坐标轴围成的三角形的面积是____________参考答案：13.正方体的内切球和外接球的半径之比为＿＿＿＿＿参考答案：正方体的棱长是内切球的直径，正方体的对角线是外接球的直径，设棱长是14.如图是一个空间几何体的三视图，根据图中尺寸（单位：cm），可知几何体表面积是．参考答案：（18+2cm2【考点】由三视图求面积、体积．【分析】通过三视图复原的几何体的特征，结合三视图的数据，求出几何体的表面积．【解答】解：由题意可知三视图复原的几何体是放倒的正三棱柱，正三角形的边长为：2，正三棱柱的高为3，所以正三棱柱的表面积为：2××2×+3×2×3=（18+2（cm2）．故答案为：（18+2cm2．15.展开式中所有系数和为M，所有二项式系数和为N，则________（用数字作答）参考答案：64略16.已知双曲线的两条渐近线均和圆C:相切,且双曲线的右焦点为圆C的圆心,则该双曲...