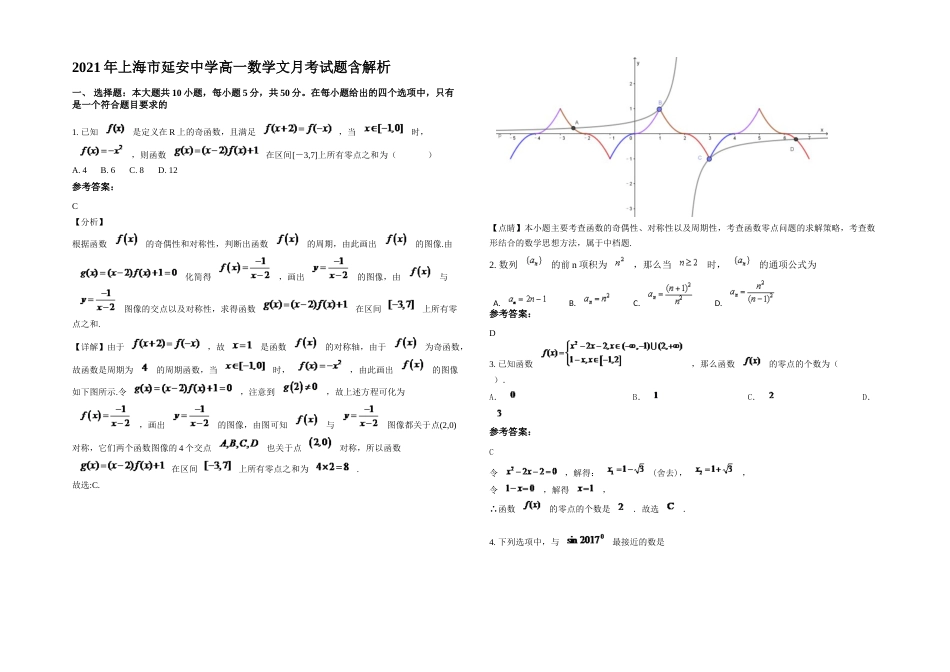
2021年上海市延安中学高一数学文月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.已知是定义在R上的奇函数，且满足，当时，，则函数在区间[－3,7]上所有零点之和为（）A.4B.6C.8D.12参考答案：C【分析】根据函数的奇偶性和对称性，判断出函数的周期，由此画出的图像.由化简得，画出的图像，由与图像的交点以及对称性，求得函数在区间上所有零点之和.【详解】由于，故是函数的对称轴，由于为奇函数，故函数是周期为的周期函数，当时，，由此画出的图像如下图所示.令，注意到，故上述方程可化为，画出的图像，由图可知与图像都关于点(2,0)对称，它们两个函数图像的4个交点也关于点对称，所以函数在区间上所有零点之和为.故选:C.【点睛】本小题主要考查函数的奇偶性、对称性以及周期性，考查函数零点问题的求解策略，考查数形结合的数学思想方法，属于中档题.2.数列的前n项积为，那么当时，的通项公式为A.B.C.D.参考答案：D3.已知函数，那么函数的零点的个数为（）．A．B．C．D．参考答案：C令，解得：(舍去)，，令，解得，∴函数的零点的个数是．故选．4.下列选项中，与最接近的数是A．B．C．D．参考答案：C5.设向量，则是的（）条件。A、充要B、必要不充分C、充分不必要D、既不充分也不必要参考答案：解析：C若则，若，有可能或为0，故选C。误解：，此式是否成立，未考虑，选A。6.已知全集U={x∈N+|2﹣＜x＜9}，M=（3，4，5），P={1，3，6}，那么{2，7，8}是（）A．M∪PB．M∩PC．（?UM）∪（?∪P）D．（?UM）∩（?UP）参考答案：D【考点】交、并、补集的混合运算．【分析】列举出全集S中的元素，根据M与P求出M与P的补集，求出两补集的并集及交集，即可做出判断．【解答】解： 全集U={1，2，3，4，5，6，7，8}，M={3，4，5}，P={1，3，6}，∴?UM={1，2，6，7，8}，?UP={2，4，5，7，8}，M∪P={1，3，4，5，6}，M∩P={3}，则（?UM）∪（?UP）={1，2，4，5，6，7，8}；（?UM）∩（?UP）={2，7，8}，故选：D．7.的值是（）A.0B.1C.2D.3参考答案：C8.关于x的不等式的解集为(－∞,1)，则关于x的不等式的解集为（）A.(1,2)B.(－1,2)C.(－∞,－1)∪(2,+∞)D.(－∞,1)∪(2,+∞)参考答案：C由已知，不等式为，所以或，故选C．9.若一个正三棱柱的三视图如下图所示，则这个正三棱柱的体积为（）A．B．C．D．参考答案：A10.已知集合,且,则的值为（）A．1B．C．1或D．1或或0参考答案：D略二、填空题:本大题共7小题,每小题4分,共28分11.若实数x，y满足，则的最大值为________．参考答案：5略12.已知幂函数的图像经过点（2，）则f(3)=.参考答案：13.已知一个扇形的周长是40，则扇形面积的最大值为___________。参考答案：略14.幂函数的图象经过点，则满足＝27的的值是．参考答案：15.已知扇形半径为8，弧长为12，则中心角为弧度，扇形面积是．参考答案：16.若，则_______．参考答案：17.过点的直线l与圆有公共点，则直线l的倾斜角的取值范围是___________．参考答案：三、解答题：本大题共5小题，共72分。解答应写出文字说明，证明过程或演算步骤18.数列{an}的前n项和为Sn，，且成等差数列．(1)求的值；(2)证明为等比数列，并求数列{an}的通项公式；(3)设，若对任意的，不等式恒成立，试求实数的取值范围．参考答案：(1);(2)见解析;(3)[1,+∞).【分析】，，又成等差数列，解得，当时，得到，代入化简，即可证得结果由得，代入化简得，讨论的取值并求出结果【详解】（1）在中令，得即，①又②则由①②解得.（2）当时，由，得到则又，则是以为首项，为公比的等比数列，，即.（3）当恒成立时，即（）恒成立设（），当时，恒成立，则满足条件；当时，由二次函数性质知不恒成立；当时，由于对称轴，则在上单调递减，恒成立，则满足条件，综上所述，实数λ的取值范围是.【点睛】本题考查了数列的综合题目，在求通项时可以采用的方法来求解，在求数列不等式时将其转化为含有参量的一元二次不等式问题，然后进行分类讨论求出结果。19.（本小题满分12分）已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα)，α∈(,).（1）若||=...