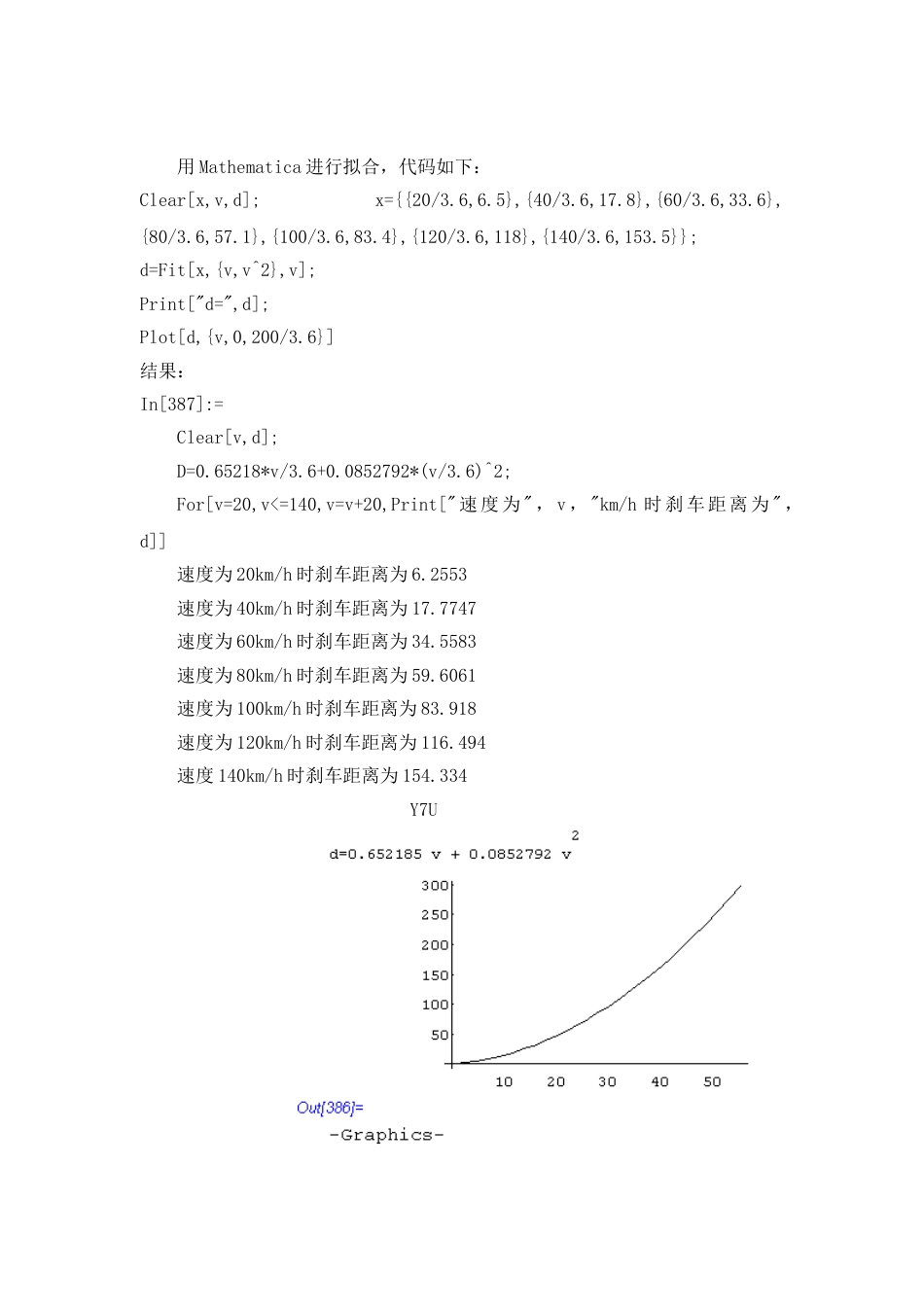
学科评价模型汽车刹车距离一、问题重述制定这样的规定是为了在后车急刹车情况下不致撞到前面的车，即要确定汽车的刹车距离。刹车距离显然与车速有关，先看看汽车在10英里/小时（约16千米/小时）的车速下2秒钟下行驶多大距离。容易计算这个距离为：10英里/小时*5280英尺/英里*1小时/3600秒*2秒=29.33英尺（=8.94米），远远大于一个车身的平均长度15英尺（=4.6米），所以“2秒准则”与上述规则并不一样。为了判断规则的合理性，需要对刹车距离做教仔细的分析。一方面，车速是刹车距离的主要影响因素，车速越快，刹车距离越长；另一方面，还有其他很多因素会影响刹车距离，包括车型.车重，刹车系统的机械状况，轮胎类型和状况，路面类型和状况，天气状况，驾驶员的操作技术和身体状况等。为了建立刹车距离与车速之间的函数关系，需要提出哪几条合理的简化假设呢？可以假设车型，轮胎类型，路面条件都相同；假设汽车没有超载;假设刹车系统的机械状况，轮胎状况，天气状况以及驾驶员状况都良好；假设汽车在平直道路上行驶，驾驶员紧急刹车，一脚把刹车踏板踩到底，汽车在刹车过程没有转方向。这些假设都是为了使我们可以仅仅考虑车速对刹车距离的影响。这些假设是初步的和粗糙的，在建模过程中，还可能提出新假设，或者修改原有假设。首先，我们仔细分析刹车的过程，发现刹车经历两个阶段：在第一阶段，司机意识到危险，做出刹车决定，并踩下刹车系统开始起作用，汽车在反应时间行驶的距离称为“反应距离”；反应距离有反应时间和车速决定，反应时间取决于司机个人状况（灵敏、机警等）和制动系统的灵敏性由于很难对反应时间进行区别，因此，通常认为反应时间为常数，而且在这段时间内车速不变。在第二阶段，从刹车踏板被踩下，刹车系统开始起作用，到汽车完全停止，汽车在制动过程“行驶”（轮胎滑动摩擦地面）的距离称为“制动距离”。刹车距离与制动作用力、车重、车速以及路面状况等因素有关系。由能量守恒制动力所做的功等于汽车动能的改变。设计制动器的一个合理原则是，最大制动力大体上与汽车的质量成正比，汽车的减速度基本上是常数。路面状况可认为是固定的。二、模型假设根据上述分析，可作如下假设：①刹车距离d等于反应距离和制动距离之和；②反应距离与车速v成正比，且比例系数为反应时间t；③刹车时使用最大制动力F，F作的功等于汽车动能的改变，且F与车质量m成正比；④人的反应时间t为一个常数；⑤在反应时间内车速v不变；⑥路面状况是固定的；⑦汽车的减速度a基本上是一个常数。三、问题分析1.由上述假设，可得：⑴；⑵,而，则。所以。综上，刹车距离的模型为。2.参数估计可用我国某机构提供的刹车距离实际观察数据来拟合未知参数t和k。转化单位后得：车速（公里/小时）20406080100120140实际刹车距离（米）6.517.833.657.183.4118.0153.5用Mathematica进行拟合，代码如下：Clear[x,v,d];x={{20/3.6,6.5},{40/3.6,17.8},{60/3.6,33.6},{80/3.6,57.1},{100/3.6,83.4},{120/3.6,118},{140/3.6,153.5}};d=Fit[x,{v,v^2},v];Print["d=",d];Plot[d,{v,0,200/3.6}]结果：In[387]:=Clear[v,d];D=0.65218*v/3.6+0.0852792*(v/3.6)^2;For[v=20,v<=140,v=v+20,Print["速度为"，v，"km/h时刹车距离为"，d]]速度为20km/h时刹车距离为6.2553速度为40km/h时刹车距离为17.7747速度为60km/h时刹车距离为34.5583速度为80km/h时刹车距离为59.6061速度为100km/h时刹车距离为83.918速度为120km/h时刹车距离为116.494速度140km/h时刹车距离为154.334Y7U3.结果分析将拟合结果与实际结果对比：（代码）Clear[v,d];d=0.65218*v/3.6+0.0852792*(v/3.6)^2;For[v=20,v<=140,v=v+20,Print["速度为",v,"km/h时刹车距离为",d]]结果：车速（公里/小时）20406080100120140实际刹车距离（米）6.517.833.657.183.4118.0153.5计算刹车距离（米）6.217.834.656.683.9116.5154.3计算刹车距离与实际刹车距离基本相当。综上，反应时间t约等于0.6522秒，刹车时减速度约等于1/2k≈6m/s2。刹车距离与车速的关系满足：d=0.6522v+0.08528v^2。四、模型的评价1、模型的优点考察误差，发现当车速不超过104.6千米/小时...