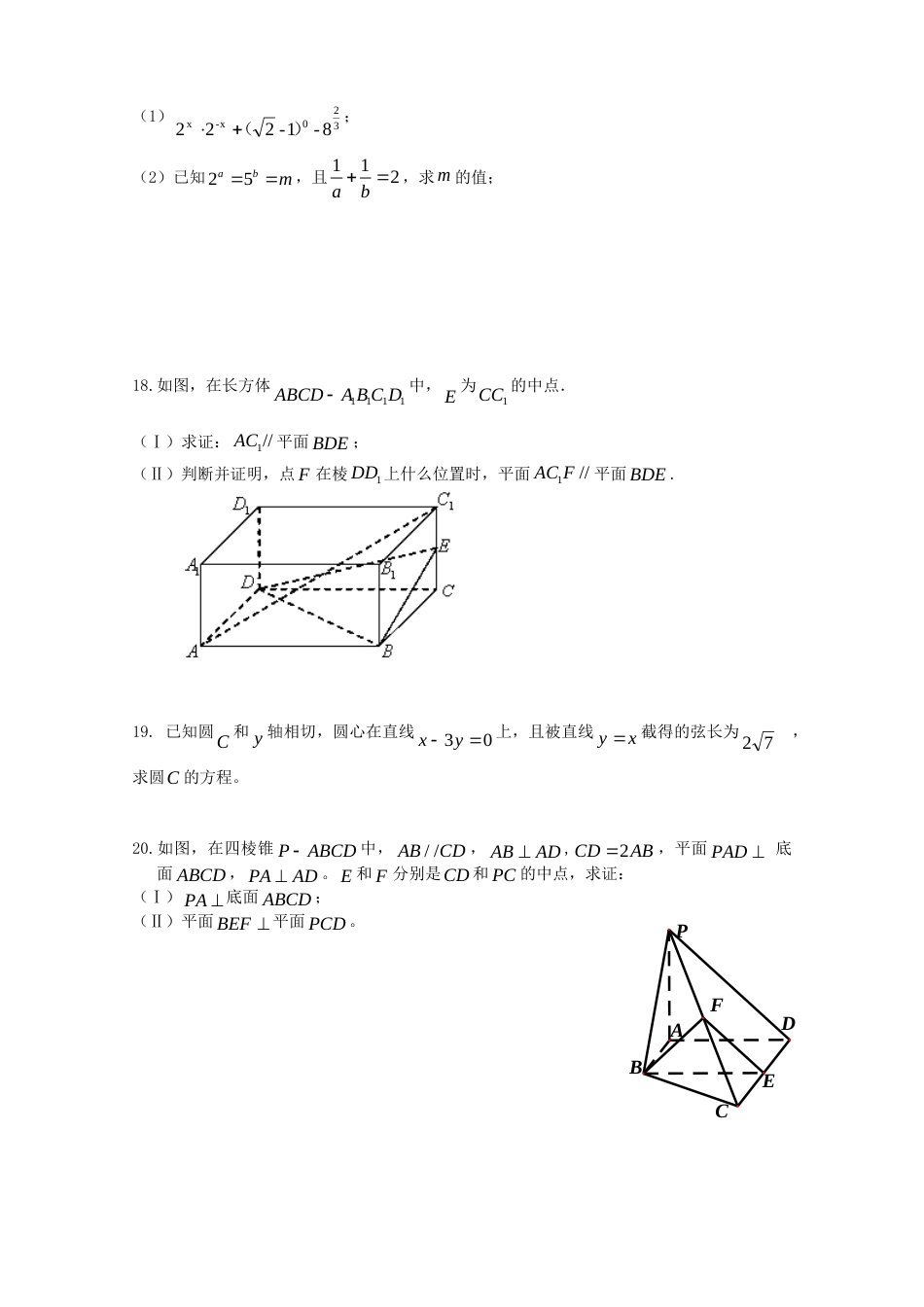
高一上学期期末考试数学试题本试卷分选择题和非选择题两部分，满分150分，考试用时120分钟．第一部分选择题（共60分）一、(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1设全集U=R，集合0}2|{2xxxA,1}{|xxb，则集合ACUB=（）A．1}{|0xxB．1}{|0xxC．2}{|0xxD．1}{|xx2.已知直线0621:axyl与01)1(:22ayaxl平行，则实数a的取值是（）A．－1或2B．0或1C．－1D．23．过两点P(2,2),Q(4,2),且圆心在直线x-y=0上的圆的标准方程是（）A.23)(3)(22yxB.23)(3)(22yxC.23)(3)(22yxD.23)(3)(22yx4．下列关于直线,lm与平面,的命题中，真命题是（）A．若l且，则lB．若l且//，则lC．若l且，则//lD．m且//lm，则//l5.函数0ln,20,32)(2xxxxxfx的零点个数为()A.0B.1C.2D.36.已知g(x)=1-2xf[g(x)]=0)(122xxx,则f(21)等于（）A．1B．3C．15D．307．若直线1l）（1xk1y和直线2l关于直线yx1对称，那么直线2l恒过定点()A．（2，0）B．（1，－1）C．（1，1）D．（－2，0）8.某几何体的三视图如图所示，则该几何体的表面积为（）A.180B.200C.220D.2409.设fx是定义在xR上以2为周期的偶函数，已知x(0,1)，12log1fxx，则函数fx在(1,2)上()A．是增函数且fx0B．是增函数且fx0C．是减函数且fx0D．是减函数且0fx8左视图410正（主）视图323俯视图10.如图，在正四棱柱1111ABCDABCD中，E，F分别是E1AB，1BC的中点，则以下结论中不成立的是（）A．EF与1BB垂直B．EF与BD垂直C．EF与CD异面D．EF与11AC异面11.直三棱柱ABC—A1B1C1的底面ABC为等腰直角三角形，斜边AB=2，侧棱AA1=1，则该三棱柱的外接球的表面积为（）.A．2B．3C．4D．512.设x1,x2是关于x的方程0122mmxx的两个不相等的实数根，那么过两点),(2Ax1x1，),(2Bx2x2的直线与圆222yx的位置关系是（）A．相切B．相离C．相交D．随m的变化而变化第二部分主观题（90分）二、填空题：本大题共4小题，每小题5分，共20分．13．无论a，b取何实数，直线ax+by+b－a＝0都过一定点P，则P点坐标为__________14.若直线xy2被圆4)(22yax所截得的弦长为22,则实数a的值为______________.15．直线1l过点(2,0)且倾斜角为30，直线2l过点(2,0)且与直线1l垂直，则直线1l与直线2l的交点坐标为_______________.16.如图，在长方形ABCD中，2AB，1BC，E为DC的中点，F为线段EC（端点除外）上一动点．现将AFD沿AF折起，使平面ABD平面ABC．在平面ABD内过点D,作DKAB，K为垂足．设AKt，则t的取值范围是．三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17.计算：ABC1A1C1D1BDF（1）320-xx-82-122）（；（2）已知25abm，且112ab，求m的值；18.如图，在长方体1111ABCDABCD中，E为1CC的中点．（Ⅰ）求证：AC1//平面BDE；（Ⅱ）判断并证明，点F在棱1DD上什么位置时，平面1ACF//平面BDE.19.已知圆C和y轴相切，圆心在直线03yx上，且被直线yx截得的弦长为27，求圆C的方程。20.如图，在四棱锥PABCD中，AB//CD，ABAD,2CDAB，平面PAD底面ABCD，PAAD。E和F分别是CD和PC的中点，求证：（Ⅰ）PA底面ABCD；（Ⅱ）平面BEF平面PCD。FCEADBP21.设二次函数2()fxaxbxc在区间2,2上的最大值、最小值分别是M、m，集合|()Axfxx．（Ⅰ）若A{1,2}，且(0)2f，求M和m的值；（Ⅱ）若A{1}，且1a，记()gaMm，求()ga的最小值．22.:已知圆M：22(2)1xy，设点,BC是直线l：20xy上的两点，它们的横坐标分别是,4()tttR，点P在线段BC上，过P点作圆M的切线PA，切点为A．（1）若0t，MP5，求直线PA的方程；（2）经过,,APM三点的圆的圆心是D，求线段DO长的最小值()Lt．