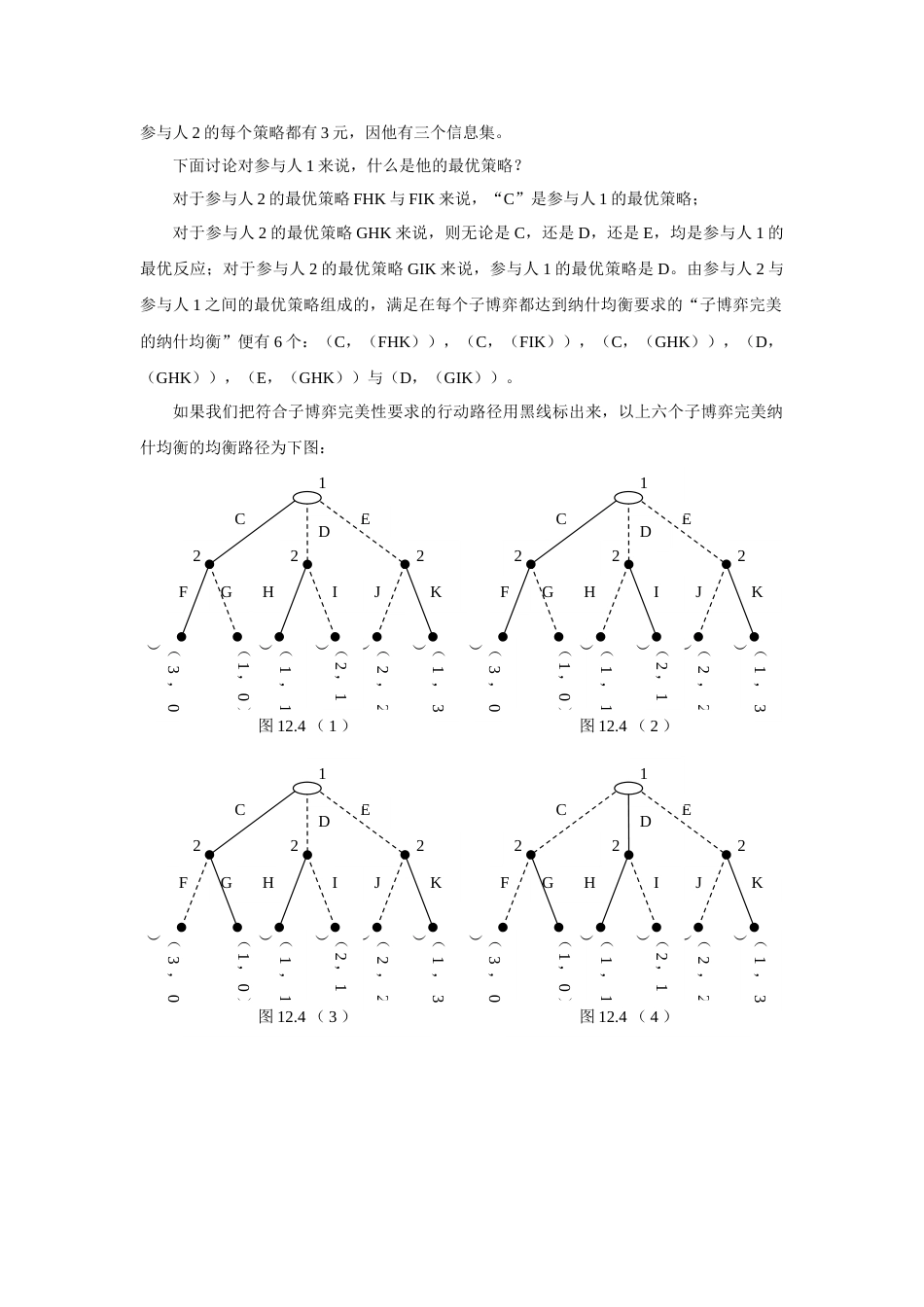
中微补充讲义（9）关于广延性博弈的几个问题一、完美信息的广延性博弈转化为策略性博弈应注意的几个问题1.策略与行动计划在广延性博弈里，如果参与人的信息集不止一个，则其策略就会成为一整套计划，参与人必须考虑到当自己处于什么“站”应当用什么应对计划的问题。这样，“策略”与“计划”就有了区别：“计划”是指参与人在某个信息集上选取的行动；而“策略”是在每个信息集上只选取一个计划的前提下，由各个信息集下所选取的一个一个行动计划构成的。2.一个策略所含的计划个数与策略集所含的策略个数为什么当完美信息的广延型博弈转化为策略性博弈时，有时策略所包含的计划个数不止一个？原因就在于参与人在广延型博弈里的信息集不止一个。参与人i的一个策略（,其中为i各用的策略个数）所含的行计划的个数等于参与人i拥有的信息集个数。i拥有n个信息集，其每一个策略便有n元。请看下例：在图11.1里，参与人“1”便有两个信息集：一个数在博弈的初始点，用空心表示；另一个信息集是在“1”走了C，参与人“2”走了E之后，又轮到“1”决策的那个信息集这里，由于信息是完美的，从而参与人“1”的每个信息集都只含有一个决策点。因此，在该博弈里，参与人1有两个信息集，而参与人2则只有1个信息集。这样，参与人2的每一个“策略”就只包含一元。即只含有一个行动计划，当“2”决策时，或者是“E”，或者是“F”。但参与人1的每个策略都必须只含有二元：即必须表示参与人1在博弈开始点的行动计划与当参与人2行动之后再由参与人1所做出的反应计划。这样，参与人1的策略就会是（C,G），（C,H)，（D,G），（D,H）这样的构成方式，其每个策略都是一套计划，而不是只含有一个计划。那么，参与人i在信息完美的广延型博弈里的策略个数是怎么决定的呢？设具有K个信息集，在第k个信息集参与人i拥有个行动计划，则i策略集中策略个数为，这里，是连乘号。在上例中，参与人1有两个信息集，且其在每个信息集都拥有两个行动计划，从而，他有四个策略：（C,G），（C,H)，（D,G），（D,H）。3.纳什均衡的精炼程度把图11.1所表示的广延型博弈转化为策略型博弈，便有表11.2：参与人2EF参（C,G）1,23,1HFGEC12（1，2）（0，0）（3，1）（2，0）Ｄ１图11.1参与人1拥有两个信息集的广延型博弈与人1（C,H）0,03,1（D,G）2,02,0（D,H）2,02,0表11.2与图11.1所对应的策略型博弈表11.2里有两个纳什均衡：一个是参与人1选D，这样无论参与人选2选E或F，无论参与人1在第二次做决策时是选G还是选H，都不会改变支付水平（2，0）。另一个纳什均衡是（（C，H），F），即参与人2用选F来结束博弈。但是，这后一个纳什均衡，如果按“反向归纳”法，是会被排除掉的。之所以要排除掉这后一个纳什均衡，是由于一旦参与人2处于自己主动采取行动的决策点，他的“理性”要求他选E，因“2”知道若我选“E”，则“1”会选G。下一章我们会详细讲“子博弈完美性”，就是分析每个决策人在每个信息集上都要讲理性，都要找出在每个信息集上的纳什均衡。而按这个原则，表11.2中的（（C，H），F）就不再是纳什均衡了。因此，当我们把完美信息的广延型博弈转化为策略型博弈时，所带来的问题是，这种转化会导致经不起仔细推敲的纳什均衡，即不够精炼的纳什均衡。二、信息完美的子博弈完美纳什均衡举例在图12.3中，长度（历史长度）为1的子博弈有3个，即由参与人2选择行动的3个子博弈。长度为2的子博弈有1个，就是原博弈本身。我们来讨论该例的子博弈完美性：由于历史之后的子博弈（最右边的那个子博弈）中，参与人2的最优行动是K，而在另外两个子博弈里，“2”的行动选择不会影响其本人的支付水平，从而，按理性原则（利己但不损人），参与人2的最优策略应该有4个：FHK，FIK，GHK，GIK。注意，（1，3）（2，2）（3，0）（1，0）（1，1）（2，1）D222IHGFCEJK1图12.3先行者在某些子博弈中有多个最优行动的广延型博弈参与人2的每个策略都有3元，因他有三个信息集。下面讨论对参与人1来说，什么是他的最优策略？对于参与人2的最优策略FHK与FIK来说，“C”是参与人1的最优策略；对于参与人2的最优策略GHK来说，则无论是C，还是D，还是E，均是...