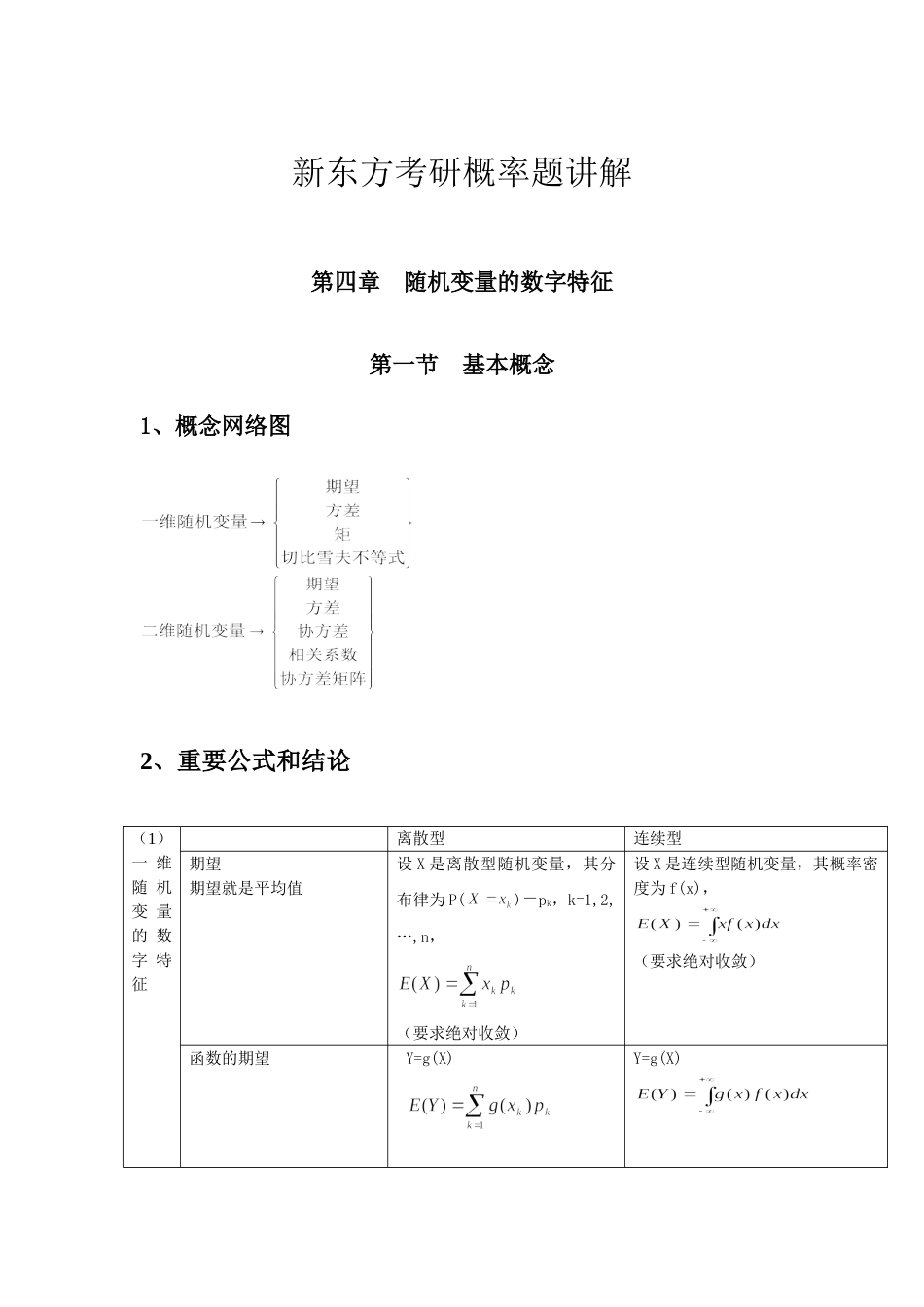
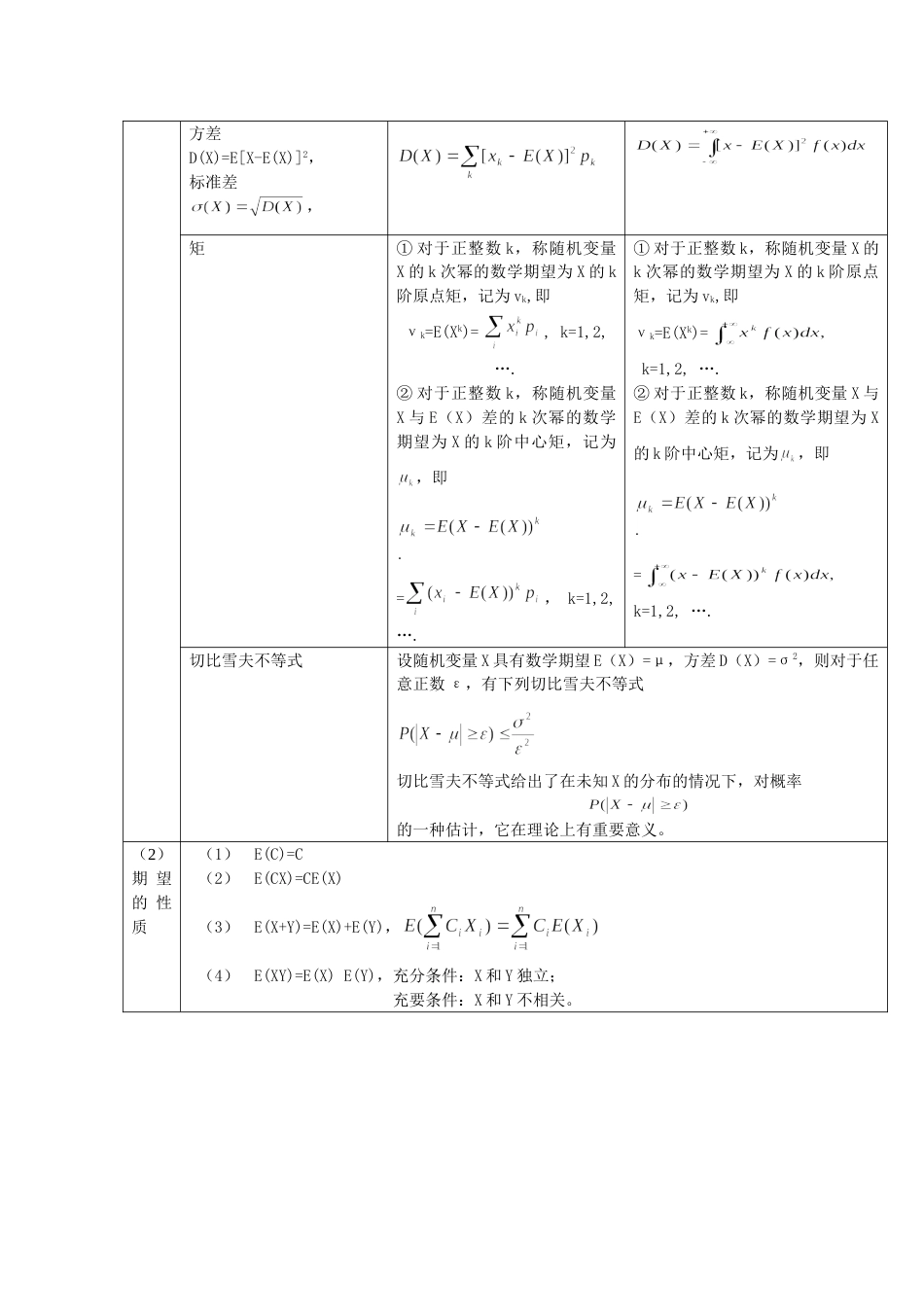
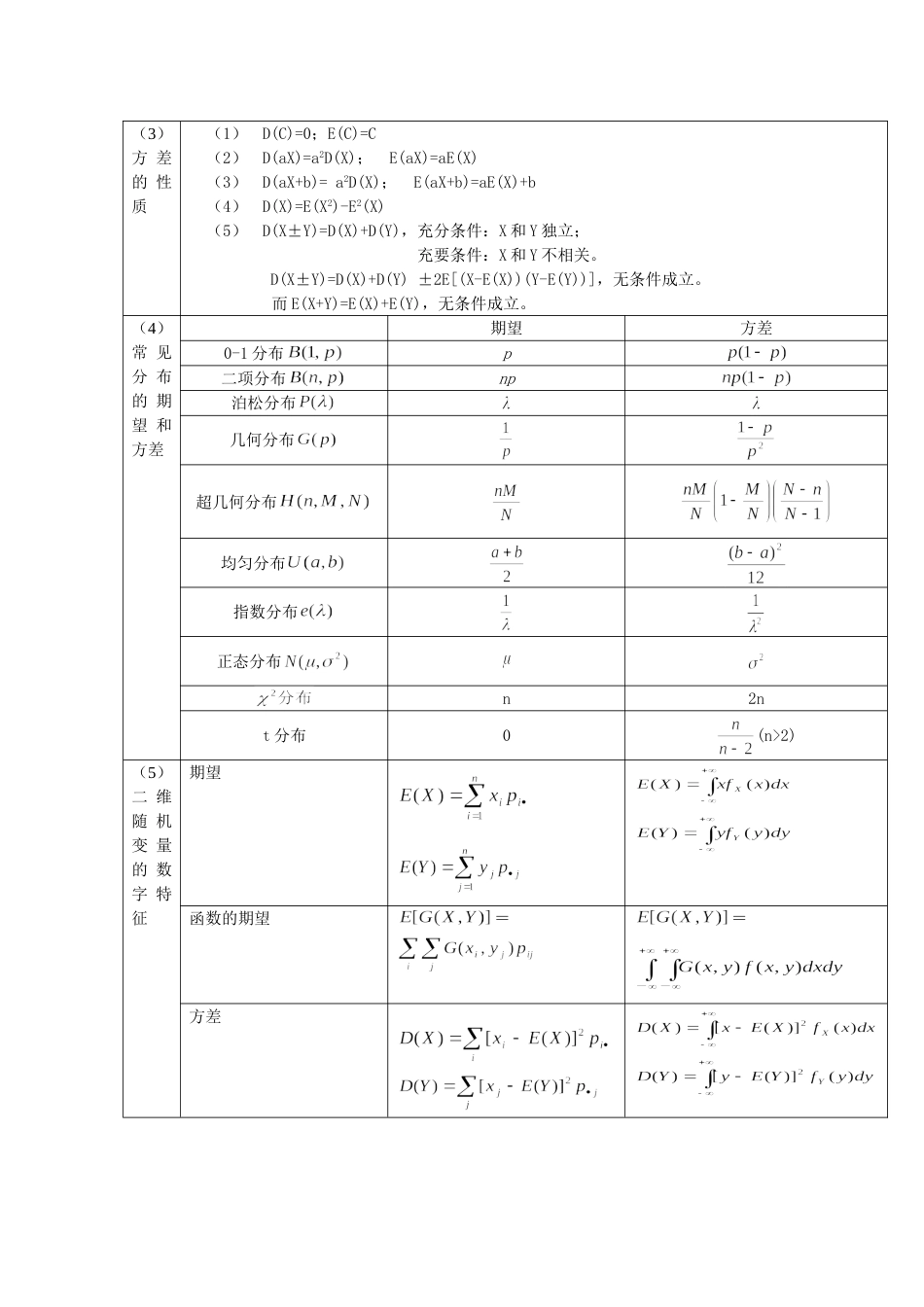
新东方考研概率题讲解第四章随机变量的数字特征第一节基本概念1、概念网络图2、重要公式和结论(1)一维随机变量的数字特征离散型连续型期望期望就是平均值设X是离散型随机变量,其分布律为P()=pk,k=1,2,…,n,(要求绝对收敛)设X是连续型随机变量,其概率密度为f(x),(要求绝对收敛)函数的期望Y=g(X)Y=g(X)方差D(X)=E[X-E(X)]2,标准差,矩①对于正整数k,称随机变量X的k次幂的数学期望为X的k阶原点矩,记为vk,即νk=E(Xk)=,k=1,2,….②对于正整数k,称随机变量X与E(X)差的k次幂的数学期望为X的k阶中心矩,记为,即=,k=1,2,….①对于正整数k,称随机变量X的k次幂的数学期望为X的k阶原点矩,记为vk,即νk=E(Xk)=k=1,2,….②对于正整数k,称随机变量X与E(X)差的k次幂的数学期望为X的k阶中心矩,记为,即=k=1,2,….切比雪夫不等式设随机变量X具有数学期望E(X)=μ,方差D(X)=σ2,则对于任意正数ε,有下列切比雪夫不等式切比雪夫不等式给出了在未知X的分布的情况下,对概率的一种估计,它在理论上有重要意义。(2)期望的性质(1)E(C)=C(2)E(CX)=CE(X)(3)E(X+Y)=E(X)+E(Y),(4)E(XY)=E(X)E(Y),充分条件:X和Y独立;充要条件:X和Y不相关。(3)方差的性质(1)D(C)=0;E(C)=C(2)D(aX)=a2D(X);E(aX)=aE(X)(3)D(aX+b)=a2D(X);E(aX+b)=aE(X)+b(4)D(X)=E(X2)-E2(X)(5)D(X±Y)=D(X)+D(Y),充分条件:X和Y独立;充要条件:X和Y不相关。D(X±Y)=D(X)+D(Y)±2E[(X-E(X))(Y-E(Y))],无条件成立。而E(X+Y)=E(X)+E(Y),无条件成立。(4)常见分布的期望和方差期望方差0-1分布p二项分布np泊松分布几何分布超几何分布均匀分布指数分布正态分布n2nt分布0(n>2)(5)二维随机变量的数字特征期望函数的期望==方差协方差对于随机变量X与Y,称它们的二阶混合中心矩为X与Y的协方差或相关矩,记为,即与记号相对应,X与Y的方差D(X)与D(Y)也可分别记为与。相关系数对于随机变量X与Y,如果D(X)>0,D(Y)>0,则称为X与Y的相关系数,记作(有时可简记为)。||≤1,当||=1时,称X与Y完全相关:完全相关而当时,称X与Y不相关。以下五个命题是等价的:①;②cov(X,Y)=0;③E(XY)=E(X)E(Y);④D(X+Y)=D(X)+D(Y);⑤D(X-Y)=D(X)+D(Y).协方差矩阵混合矩对于随机变量X与Y,如果有存在,则称之为X与Y的k+l阶混合原点矩,记为;k+l阶混合中心矩记为:(6)协方差的性质(i)cov(X,Y)=cov(Y,X);(ii)cov(aX,bY)=abcov(X,Y);(iii)cov(X1+X2,Y)=cov(X1,Y)+cov(X2,Y);(iv)cov(X,Y)=E(XY)-E(X)E(Y).(7)独立和不相关(i)若随机变量X与Y相互独立,则;反之不真。(ii)若(X,Y)~N(),则X与Y相互独立的充要条件是X和Y不相关。例4.1:箱内装有5个电子元件,其中2个是次品,现每次从箱子中随机地取出1件进行检验,直到查出全部次品为止,求所需检验次数的数学期望。例4.2:将一均匀骰子独立地抛掷3次,求出现的点数之和的数学期望。例4.3:袋中装有标着1,2,…,9号码的9只球,从袋中有放回地取出4只球,求所得号码之和X的数学期望。例4.4:设随机变量X的概率密度为求E(X)及D(X)。例4.5:设随机变量X~N(0,4),Y~U(0,4),且X,Y相互独立,求E(XY),D(X+Y)及D(2X-3Y)。例4.6:罐中有5颗围棋子,其中2颗为白子,另3颗为黑子,如果有放回地每次取1子,共取3次,求3次中取到的白子次数X的数学期望与方差。例4.7:在上例中,若将抽样方式改为不放回抽样,则结果又是如何?例4.8:“随机变量X的数学期望E(X)=μ.”的充分条件:(1)X的密度函数为f(x)=(λ>0,-∞<x<+∞)(2)X的密度函数为,(x)例4.9:利用切比雪夫不等式估计随机变量与其数学期望之差大于3倍标准差的概率。例4.10:设随机变量X和Y的方差存在且不等于0,则D(X+Y)=D(X)+D(Y)是X和Y()。(A)不相关的充分条件,且不是必要条件;(B)独立的充分条件,但不是必要条件;(C)不相关的充分必要条件;(D)独立的充分必要条件。例4.11:设X与Y相互独立都服从P(λ),令U=2X+Y,V=2X-Y。求随机变量U和V的相关系数例4.12:设(X,Y)服从D={(x,y)|x2+y2≤1|}上的均匀分布,求并且讨论X与...