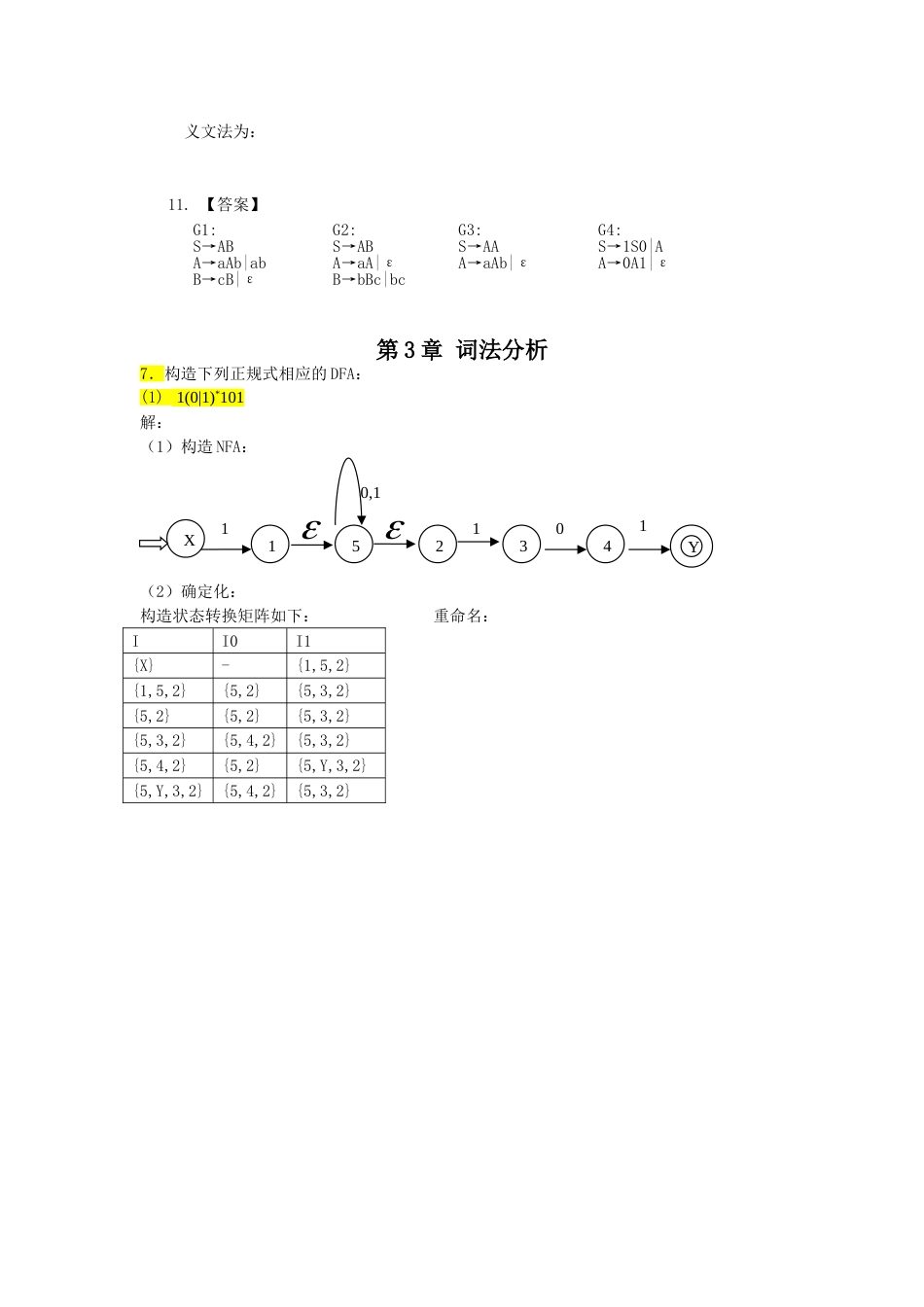
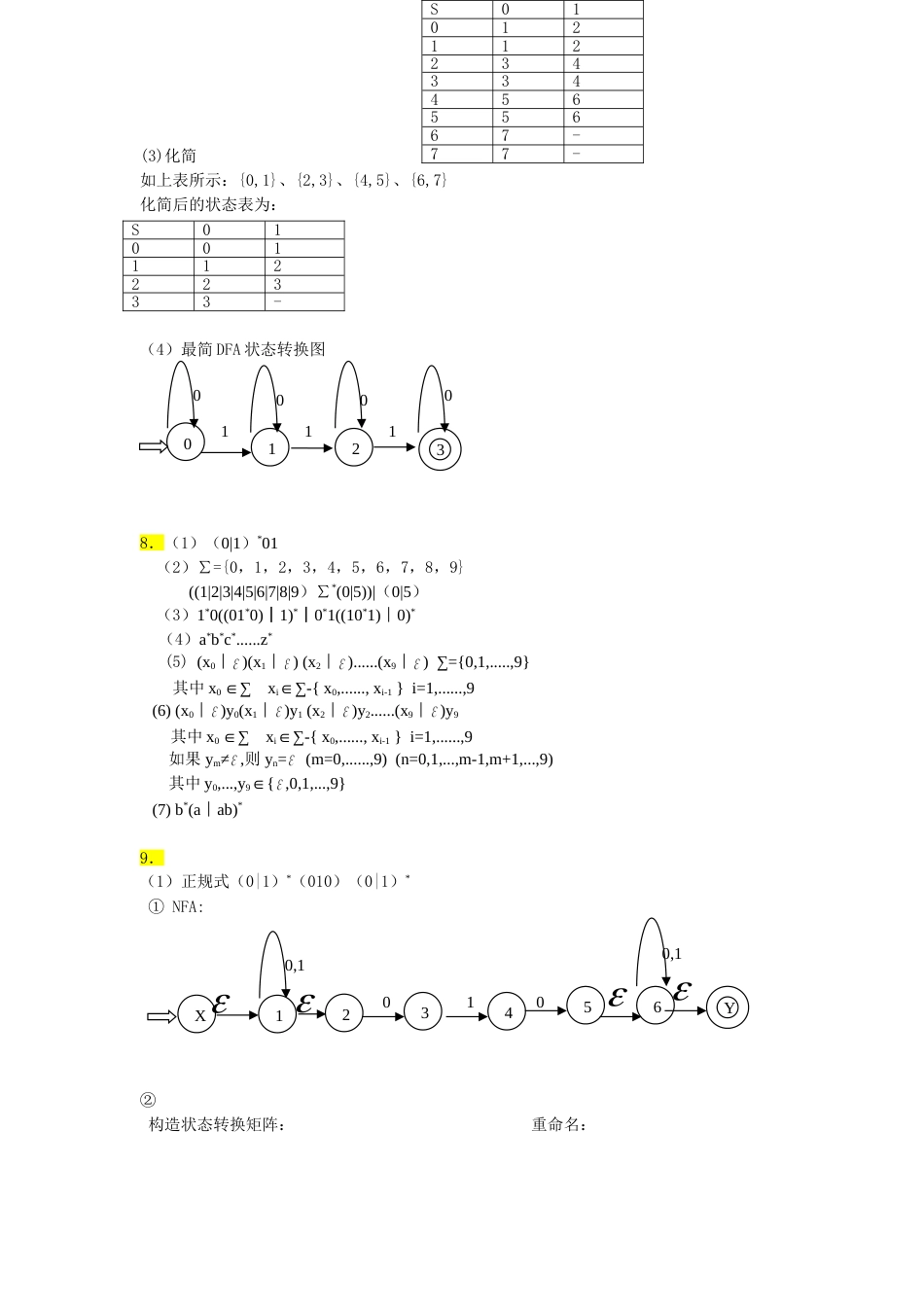
第二章高级语言及其语法描述6．（1）L（G6）={0,1,2,......,9}+（2）最左推导：N=>ND=>NDD=>NDDD=>DDDD=>0DDD=>01DD=>012D=>0127N=>ND=>DD=>3D=>34N=>ND=>NDD=>DDD=>5DD=>56D=>568最右推导：N=>ND=>N7=>ND7=>N27=>ND27=>N127=>D127=>0127N=>ND=>N4=>D4=>34N=>ND=>N8=>ND8=>N68=>D68=>5687．【答案】Ｇ：S→ABC|AC|CA→1|2|3|4|5|6|7|8|9B→BB|0|1|2|3|4|5|6|7|8|9C→1|3|5|7|98．（1）最左推导：E=>E+T=>T+T=>F+T=>i+T=>i+T*F=>i+F*F=>i+i*F=>i+i*iE=>T=>T*F=>F*F=>i*F=>i*(E)=>i*(E+T)=>i*(T+T)=>i*(F+T)=>i*(i+T)=>i*(i+F)=>i*(i+i)最右推导：E=>E+T=>E+T*F=>E+T*i=>E+F*i=>E+i*i=>T+i*i=>F+i*i=>i+i*iE=>T=>T*F=>T*(E)=>T*(E+T)=>T*(E+F)=>T*(E+i)=>T*(T+i)=>T*(F+i)=>T*(i+i)=>F*(i+i)=>i*(i+i)(2)9．证明：该文法存在一个句子iiiei有两棵不同语法分析树，如下所示，因此该文法是二义的。10.【答案】无二E+TTFiEE+TFiFiE+TFiET*FiFiTE-TTFiEE-TFiFiSSeiSiSSiiSeiSiSiSiS→TS|TT→(S)|()义文法为：11.【答案】第3章词法分析7．构造下列正规式相应的DFA：(1)1(0|1)*101解：（1）构造NFA：（2）确定化：构造状态转换矩阵如下：重命名：II0I1{X}-{1,5,2}{1,5,2}{5,2}{5,3,2}{5,2}{5,2}{5,3,2}{5,3,2}{5,4,2}{5,3,2}{5,4,2}{5,2}{5,Y,3,2}{5,Y,3,2}{5,4,2}{5,3,2}0X152Y0,113411G1:S→ABA→aAb|abB→cB|εG2:S→ABA→aA|εB→bBc|bcG3:S→AAA→aAb|εG4:S→1S0|AA→0A1|ε(3)化简(4)化简之后的状态表分组{0,1,2,3,4}{5}考察{0,1,2,3,4}0={2,4}{0,1,2,3,4}1={1,3,5}∴分化为：{0,1,2,3}、{4}、{5}再考察：{0,1,2,3}0={2,4}∴分化为：{0,1,2,}、{3}、{4}、{5}再考察：{0,1,2}0={2}{0,1,2}1={1,3}∴分化为：{0}、{1,2,}、{3}、{4}、{5}(5)画出状态转换图：(3)0*10*10*10*解：（1）构造NFA：（2）确定化：构造状态转换矩阵如下：重命名：II0I1{X,7,1}{7,1}{2,8,3}{7,1}{7,1}{2,8,3}{2,8,3}{8,3}{4,9,5}{8,3}{8,3}{4,9,5}{4,9,5}{9,5}{6,10,Y}{9,5}{9,5}{6,10,Y}{6,10,Y}{10,Y}--{10,Y}{10,Y}--S010-1123223343425543S010-11122323144320121013010410111X712Y8349561010000(3)化简如上表所示：{0,1}、{2,3}、{4,5}、{6,7}化简后的状态表为：（4）最简DFA状态转换图8．（1）（0|1）*01（2）∑={0，1，2，3，4，5，6，7，8，9}((1|2|3|4|5|6|7|8|9）∑*(0|5))|（0|5）（3）1*0((01*0)︱1)*︱0*1((10*1)︱0)*（4）a*b*c*......z*(5)(x0︱)(x1︱)(x2︱)......(x9︱)∑={0,1,.....,9}其中x0∈∑xi∈∑-{x0,......,xi-1}i=1,......,9(6)(x0︱)y0(x1︱)y1(x2︱)y2......(x9︱)y9其中x0∈∑xi∈∑-{x0,......,xi-1}i=1,......,9如果ym≠,则yn=(m=0,......,9)(n=0,1,...,m-1,m+1,...,9)其中y0,...,y9∈{,0,1,...,9}(7)b*(a︱ab)*9．（1）正规式（0|1）*（010）（0|1）*①NFA:②构造状态转换矩阵：重命名：S0101211223433445655667-77-S0100111222333-012311100000,10,101X12Y34560③最小化④化简后的状态表分组：{0,1,2,3}、{4,5,6,7}考察：{0,1,2,3}0={1,4}∴分化为{0,1,2}、{3}、{4,5,6,7}再考察：{0,1,2}0={1}{0,1,2}1={2,3}∴分化为{0,2}、{1}、{3}、{4,5,6,7}再考察：{4,5,6,7}0={4,5}{4,5,6,7}1={6,7}∴分化为{0,2}、{1}、{3}、{4,5,6,7}再重新命名为：{0,2}—0、{1}—1、{3}—2、{4,5,6,7}—3最小化后的状态转换图为：（2）正规式1*（0︱11︱111）*1*或1*（0︱111*）*1*①NFA:II0I1{X,1,2}{1,3,2}{1,2}{1,3,2}{1,3,2}{1,4,2}{1,2}{1,3,2}{1,2}{1,4,2}{1,5,3,2,6,Y}{1,2|{1,5,3,2,6,Y}{1,3,6,2,Y}{1,4,6,2,Y}{1,3,6,2,Y}{1,3,6,2,Y}{1,4,6,2,Y}{1,4,6,2,Y}{1,5,3,2,6,Y}{1,6,2,Y}{1,6,2,Y}{1,3,6,2,Y}{1,6,2,Y}S01012113212342456556647757S010101122303330011201010，13②构造状态转换矩阵：重命名：③最小化④化简后的状态表分组{0,1,2,4,5,6,7}、{3}考察：{0,1,2,4,5,6,7}0={1}{0,1,2,4,5,6,7}1={2,3,4,6,7}∴分化为{0,2,4,5,6,7}、{1}、{3}再重新命名为：{0,2,4,5,6,7}—0、{1}—1、{3}—2最小化后的状态转换图为：12．（a）1011X123Y45678...