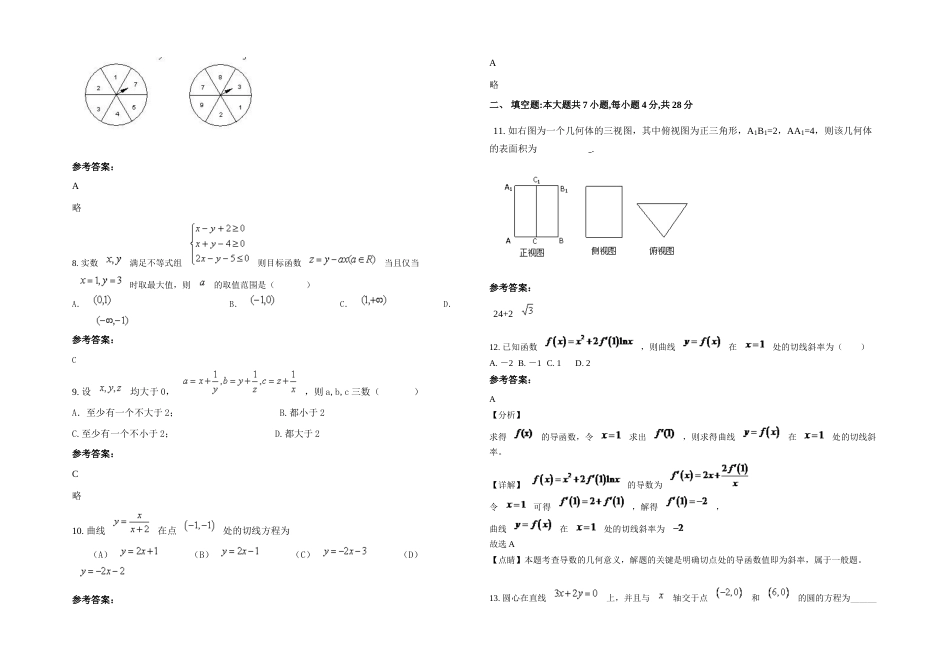
重庆沙河中学2020年高二数学理上学期期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.的值为()参考答案：D2.设，则“”是“”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件参考答案：A分析：首先求解绝对值不等式，然后求解三次不等式即可确定两者之间的关系.详解：绝对值不等式，由.据此可知是的充分而不必要条件.本题选择A选项.点睛：本题主要考查绝对值不等式的解法，充分不必要条件的判断等知识，意在考查学生的转化能力和计算求解能力.3.等比数列中，，则（）A．B．C．D．参考答案：D4.若变量满足约束条件，A.B．C．D．参考答案：C略5.已知函数是定义在R上的奇函数，且满足当时，，则使的的值是（）A．B．C．D．参考答案：D略6.某考察团对全国10大城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查，y与x具有相关关系，回归方程为＝0.66x＋1.562.若某城市居民人均消费水平为7.675千元，估计该城市人均消费额占人均工资收入的百分比约为()A．83%B．72%C．67%D．66%参考答案：A试题分析：将y＝7.675代入回归方程，可计算得x≈9.26，所以该城市人均消费额占人均工资收入的百分比约为7.675÷9.26≈0.83，即约为83%.考点：回归方程7.如图所示，在两个圆盘中，指针在本圆盘每个数所在区域的机会均等，那么两个指针同时落在奇数所在区域的概率是（）（A）．（B）．（C）．（D）．参考答案：A略8.实数满足不等式组则目标函数当且仅当时取最大值，则的取值范围是（）A．B．C．D．参考答案：C9.设均大于0，，则a,b,c三数（）A．至少有一个不大于2；B.都小于2C.至少有一个不小于2；D.都大于2参考答案：C略10.曲线在点处的切线方程为（A）（B）（C）（D）参考答案：A略二、填空题:本大题共7小题,每小题4分,共28分11.如右图为一个几何体的三视图，其中俯视图为正三角形，A1B1=2，AA1=4，则该几何体的表面积为.参考答案：24+212.已知函数，则曲线在处的切线斜率为（）A.－2B.－1C.1D.2参考答案：A【分析】求得的导函数，令求出，则求得曲线在处的切线斜率。【详解】的导数为令可得，解得，曲线在处的切线斜率为故选A【点睛】本题考查导数的几何意义，解题的关键是明确切点处的导函数值即为斜率，属于一般题。13.圆心在直线上，并且与轴交于点和的圆的方程为_____________．参考答案：略14.将直线y＝－x+2绕点(2,0)按顺时针方向旋转60°所得的直线在y轴上的截距是_________参考答案：15.高为5m和3m的两根旗杆竖在水平地面上,且相距10m,如果把两旗杆底部的坐标分别确定为,,则地面观测两旗杆顶端仰角相等的点的轨迹方程是________.参考答案：4x2+4y2-85x+100=016.某班准备从含甲、乙的7名男生中选取4人参加接力赛，要求甲、乙两人至少有一人参加，且若甲、乙同时参加,则他们在赛道上顺序不能相邻，那么不同的排法种数为。参考答案：600略17.若0<a<1，则不等式的解集是________________。参考答案：三、解答题：本大题共5小题，共72分。解答应写出文字说明，证明过程或演算步骤18.已知集合{(x,y)|x∈［0,2］,y∈［-1,1］}.(1)若x,y∈Z，求x+y≥0的概率；(2)若x,y∈R，求x+y≥0的概率.参考答案：(1)设事件“x+y≥0,x,y∈Z”为Ax,y∈Z,x∈［0,2］，即x=0,1,2;y∈［-1,1］,即y=-1,0,1则基本事件如表，基本事件总和n=9，其中满足“x+y≥0”的基本事件n=8P(A)=故x，y∈Z,x+y≥0的概率为.(2)设事件“x+y≥0,x,y∈R”为B,x∈［0,2］，y∈［-1,1］基本事件用下图四边形ABCD区域表示，SABCD=2×2=4事件B包括的区域如阴影部分S阴影=SABCD-,故x,y∈R，x+y≥0的概率为略19.过点（0，4），斜率为﹣1的直线与抛物线y2=2px（p＞0）交于两点A、B，且弦|AB|的长度为4．（1）求p的值；（2）求证：OA⊥OB（O为原点）．参考答案：（1）解：直线方程为y=﹣x+4，联立方程消去y得，x2﹣2（p+4）x+16=0．设A（x1，y1），B（x2，y2），得x1+x2=2（p+4），x1x2=16，△=4（p+2）2﹣64＞0．所以|AB|=|x1﹣x2|==4，所以p=2．（2）证明：由（1）知，x1+x2=2（p+4）=12，x1x2=16，∴y1y2=（﹣x1+4）（﹣x2+4）...