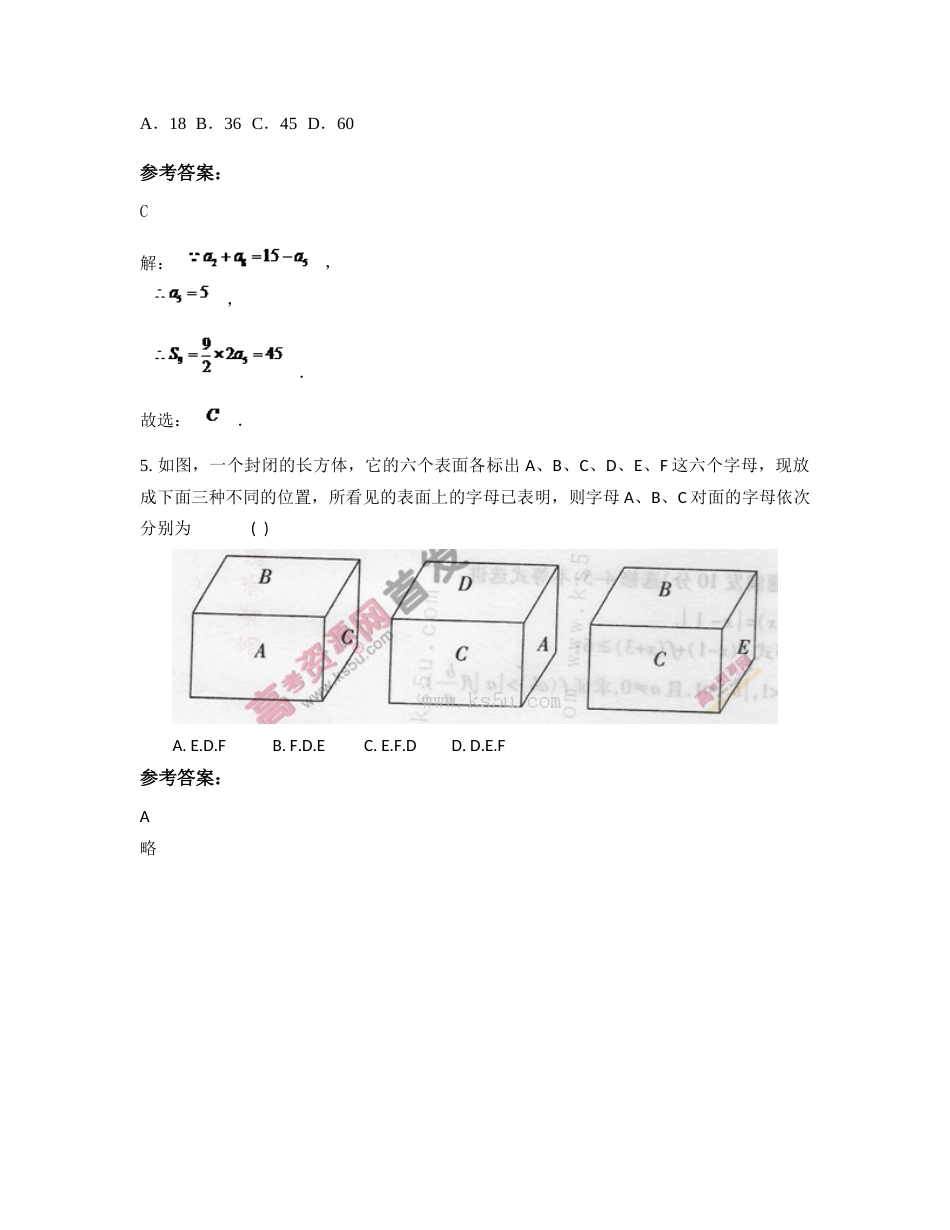
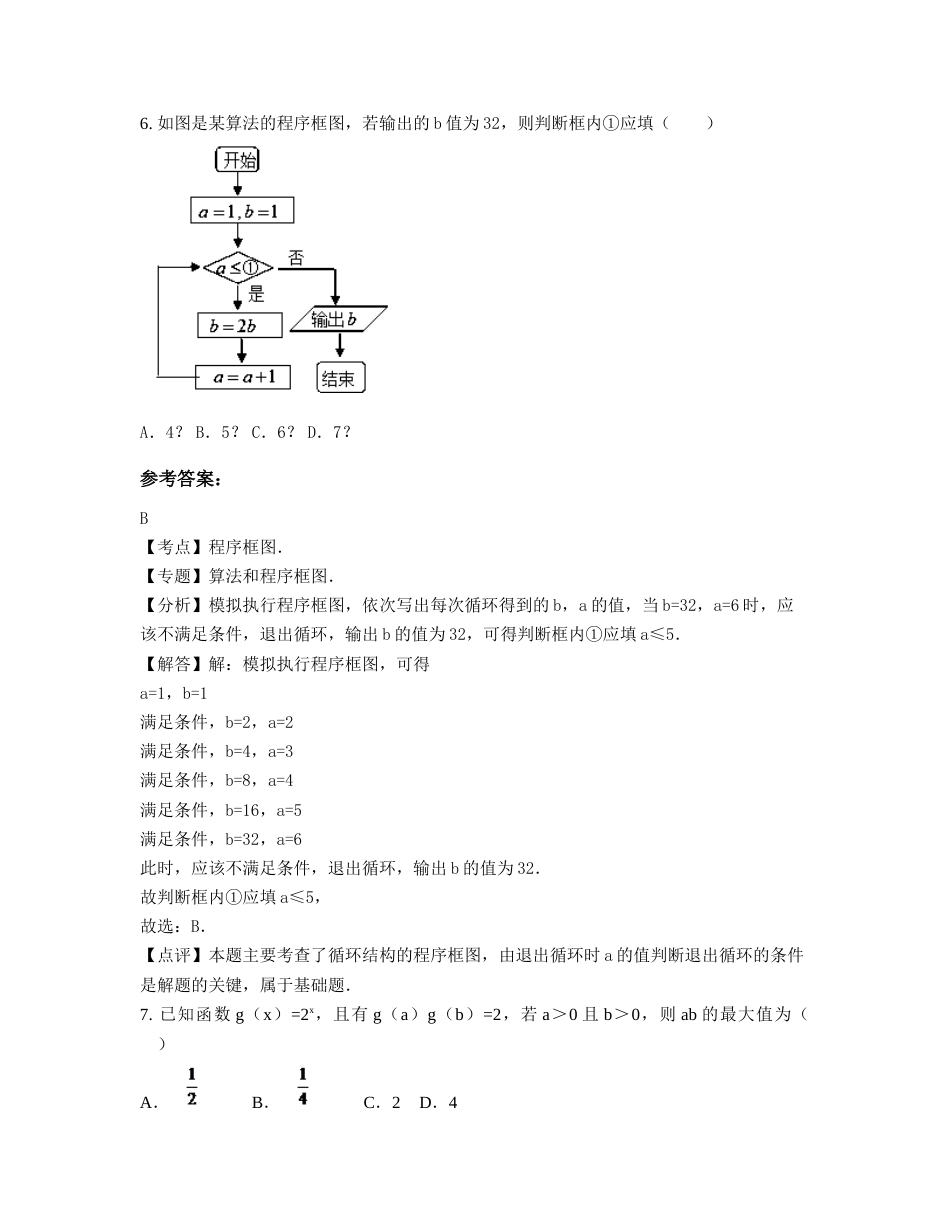
江苏省徐州市睢宁县新世纪中学高三数学理月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.已知边长为1的正方形ABCD位于第一象限，且顶点A、D分别在x、y的正半轴上(含原点)滑动，则的最大值是()参考答案：C略2.若函数=的定义域为,则实数的取值范围是（）A、(－∞,+∞)B、[0,C、(,+∞)D、(0,参考答案：B略3.焦点在轴上的椭圆离心率为，则的值为（A）（B）（C）（D）参考答案：答案：D4.设等差数列{an}的前n项和为Sn，若，则等于A．18B．36C．45D．60参考答案：C解：，，．故选：．5.如图，一个封闭的长方体，它的六个表面各标出A、B、C、D、E、F这六个字母，现放成下面三种不同的位置，所看见的表面上的字母已表明，则字母A、B、C对面的字母依次分别为()A.E.D.FB.F.D.EC.E.F.DD.D.E.F参考答案：A略6.如图是某算法的程序框图，若输出的b值为32，则判断框内①应填（）A．4？B．5？C．6？D．7？参考答案：B【考点】程序框图．【专题】算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的b，a的值，当b=32，a=6时，应该不满足条件，退出循环，输出b的值为32，可得判断框内①应填a≤5．【解答】解：模拟执行程序框图，可得a=1，b=1满足条件，b=2，a=2满足条件，b=4，a=3满足条件，b=8，a=4满足条件，b=16，a=5满足条件，b=32，a=6此时，应该不满足条件，退出循环，输出b的值为32．故判断框内①应填a≤5，故选：B．【点评】本题主要考查了循环结构的程序框图，由退出循环时a的值判断退出循环的条件是解题的关键，属于基础题．7.已知函数g（x）=2x，且有g（a）g（b）=2，若a＞0且b＞0，则ab的最大值为（）A．B．C．2D．4参考答案：B【考点】基本不等式；指数式与对数式的互化．【分析】先根据条件得出a+b=1，再应用均值不等式可以把条件转化为关于的不等式，进而解出ab的取值范围．【解答】解： 函数g（x）=2x，且有g（a）g（b）=2，∴2a?2b=2?a+b=1， a，b∈（0，+∞），∴a+b，即2≤1，当且仅当a=b时取等号，解得ab≤，故选B．8.若等比数列的公比为2，但前4项和为1，则这个等比数列的前8项和等于（）A．21B．19C．17D．15参考答案：答案：C9.已知集合，则（）A．B．2，{(3,2),(2,0)}C．{3,2}D．[－3,3]参考答案：D,,所以,选D.10.已知函数，则（）A.函数f(x)的图像关于对称B.函数f(x)的图像关于对称C.函数f(x)的图像关于(2,2)对称D.函数f(x)的图像关于(4,4)对称参考答案：C【分析】根据函数的解析式，易得函数过原点，从而根据选项进行一一验证，即可得答案.【详解】 函数过点，对A，若函数的图像关于对称，则，显然不成立，故A错误；对B，若函数的图像关于对称，则，显然不成立，故B错误；对D，若函数的图像关于对称，则，显然不成立，故D错误；利用排除法可得C正确；故选：C.【点睛】本题考查函数的对称性应用，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意利用排除法进行解题.二、填空题:本大题共7小题,每小题4分,共28分11.（x+）（2x﹣）5的展开式中各项系数的和为2，则该展开式中常数项为．参考答案：40【分析】由于二项式展开式中各项的系数的和为2，故可以令x=1，建立起a的方程，解出a的值来，然后再由规律求出常数项【解答】解：由题意，（x+）（2x﹣）5的展开式中各项系数的和为2，所以，令x=1则可得到方程1+a=2，解得得a=1，故二项式为由多项式乘法原理可得其常数项为﹣22×C53+23C52=40故答案为4012.阅读如图所示的程序框图，运行相应的程序.若输入的值为2，则输出的结果.参考答案：13.△ABC的内角A，B，C所对的边分别为a，b，c，a=4，c=，sinA=4sinB，则C=_．参考答案：14.已知定义域为I的函数f（x），若存在开区间（a，b）?I和正的常数c，使得任意x∈（a，b）都有﹣c＜f（x）＜c，且对任意x?（a，b）都有|f（x）|=c恒成立，则称f（x）为区间I上的“Z型”函数，给出下列函数：①f（x）=；②f（x）=；③f（x）=|sinx|；④f（x）=x+cosx，其中是区间I上的“Z型”函数的是（只需写出序号即可）参考答案：①【考点】函数的值．【分析】①根据题中的定...