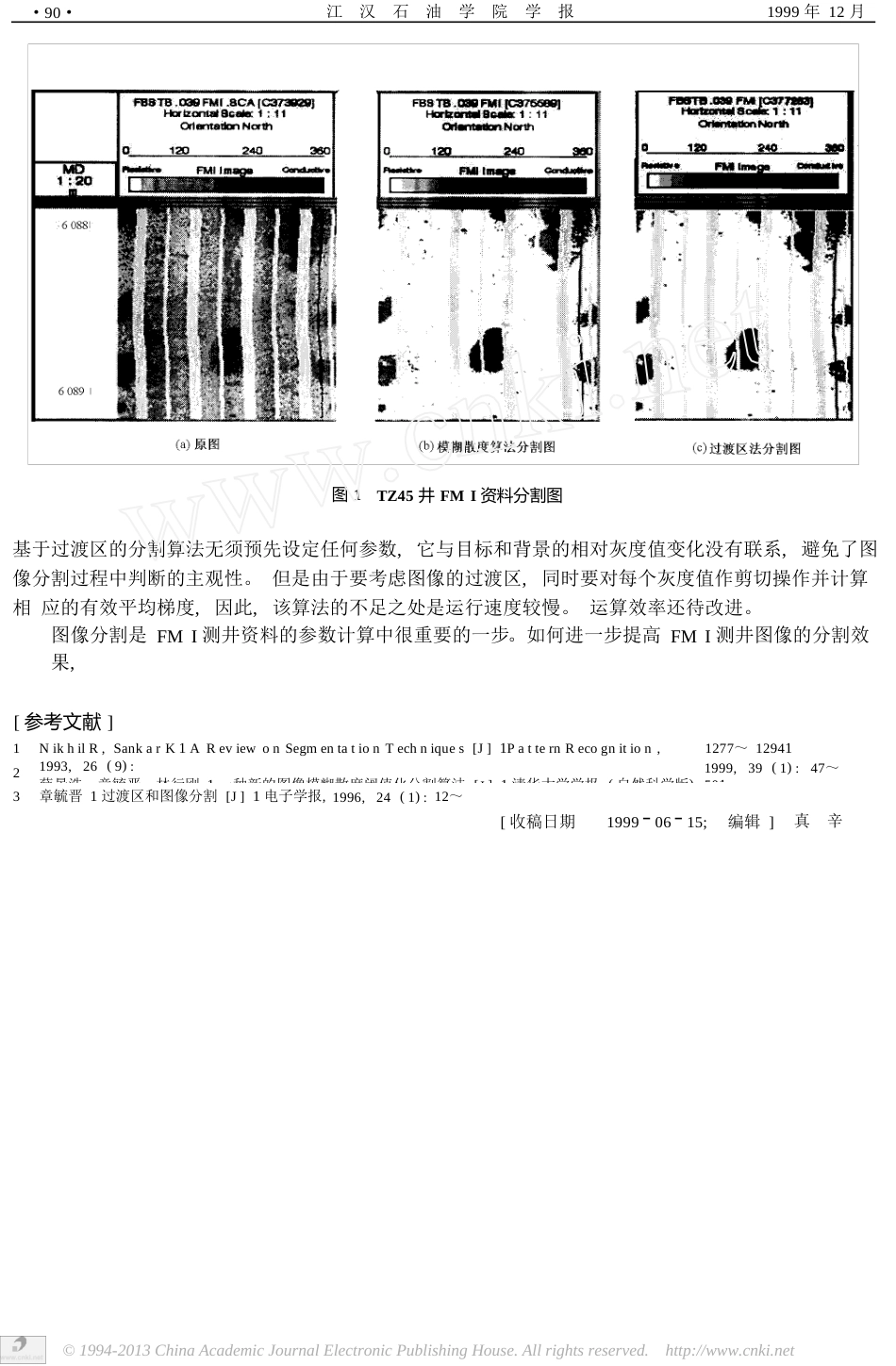
两种图像分割算法在FMI成像资料中的应用张丽莉,刘瑞林(江汉石油学院地球物理勘探系,湖北荆州434102)[摘要]为了从地层微电阻率扫描成像测井(FMI)图像中分割出主要反映裂缝、孔洞的子图像,介绍了两种图像分割算法:一种是基于图像间模糊散度的阈值化算法,另一种是基于过渡区的分割算法。并分别用这两种分割算法对塔里木盆地中央隆起TZ45井FMI图像进行分割。研究结果表明,这两种算法对FMI成像测井资料获得了较好的分割效果。[中图分类号]P631184[文献标识码]A[文章编号10009752(1999)04008803目前,对地层微电阻率扫描成像测井(FMI)资料的应用主要局限于孔洞、裂缝的定性识别和地层倾角解释等方面。对于FMI资料的图像处理和定量参数提取方面,国内外都处于研究、试验阶段。为了从FMI资料中提取定量信息,如面孔率、裂缝长度等参数,一个重要的步骤就是要对FMI图像数据进行分割,以期从实际FMI资料中分离出反映孔洞、裂缝的子图像。FMI图像分割的结果直接影响参数计算的准确性。然而,有关图像分割的技术与方法主要针对光学扫描图像进行的1。FMI成像测井资料与光扫描图像不同。FMI图像值是所测量的地质体的电导率值。在不同地质体(如基岩与孔洞)的边界处,测量值不是陡变的,而是存在明显的过渡区。另外,含孔洞、裂缝的地层的FMI成像测井图像可以认为由目标(孔洞等)和背景(基岩)两类组成,目标与背景的灰度值主要集中在相应的均值附近。因此,FMI测井图像可以通过灰度特征进行分割。笔者根据FMI图像的这一特征,应用两种图像分割算法(一种基于图像间模糊散度的阈值化算法,另一种是基于过渡区的分割算法),对FMI图像进行了试验。1两种图像分割算法的基本原理111图像间模糊散度的阈值化分割算法图像间模糊散度的阈值化分割算法是一种采用模糊集合分别表达分割前后的图像,通过最小模糊散度准则2实现图像分割中最优阈值提取的算法。最小模糊散度准则:选择最优阈值使其满足使原始图和分割图的信息距离量最小的条件,即要求最优阈值满足使原始图与分割图之间的模糊散度最小。用P与Q分别表征分割前后的图像。若将P与Q定义成论域S上的两个模糊集合,则{up(s)fs∈S}{uq(s)fs∈S}P=Q=式中,up(s),uq(s)分别是P,Q的隶属度函数,满足0≤up(s),uq(s)≤1。在图像分割的应用中,论域S取灰度轴,元素s取像素点的灰度。在一幅图像内,目标与背景的灰度主要集中在目标类与背景类的均值附近,即均值的隶属度最高(为1),类内像素的隶属度和该像素到均值的距离成反比,而且类内(外)所有像素的隶属度应该大于(小于)015。对未分割的原始图G而言,满足上述思想的目标的隶属度函数u1(x;t,G)和背景的隶属度函数u2(x;t,G)分别为x-m1(t)a10≤x≤t1-2Cu1(x;t,G)=u2(x;t,G)=1-u1(x;t,G)(1)a1x-m2(t)0<x≤L2C[作者简介]张丽莉(1975),女,1997江汉石油学院毕业,在读硕士生,现从事成像测井应用的研究工作。刘瑞林,钟广法,周云才1FMI、ARI成像测井资料定量计算储层参数方法研究及应用1塔里木油田公司与江汉石油学院研究报告第21卷第4期张丽莉等:两种图像分割算法在FMI成像资料中的应用·89·式中,t为待选阈值;L为灰度上界;a为类内元素对均值的紧致度参数,可描述诸如大约、接近、相似等模糊语义,a≥0;常数C为归一化因子;m1(t),m2(t)分别为类内目标和背景的均值,其值由直方图估计。而分割后的二值图B的目标、背景模糊隶属度函数分别为0≤x≤tt<x≤L10u1(x;t,B)=u2(x;t,B)=1-u1(x;t,B)(2)原始图G和分割后二值图B之间的模糊散度既定量反映了类内成员对该类的隶属程度,又表征了两个类之间的相似程度。按照最小模糊散度准则,可以穷举搜索一个使模糊散度最小的最优阈值t。对FMI资料的试验表紧致度参数a取015较合适。因实际处理的FMI数据刻度到0,112过渡区的分割算法的范围,故归一化因子C取511。511图像中目标与背景之间的边界其实也是一个特殊的区域。它既有边界的特点——把不同的区域分开,也有区域的特点——其自身有宽度,面积不为零。这个特殊的区域称作过渡区3。过渡区包含的像素值一般也在相应的目标和背景之间。过渡区可借助于图像有效平均梯度(g)和对图像灰度的剪切操作来确定3。设以f(i,j)代表在二维空间变化的图像函数,其中i,j属于表示像素空间坐...