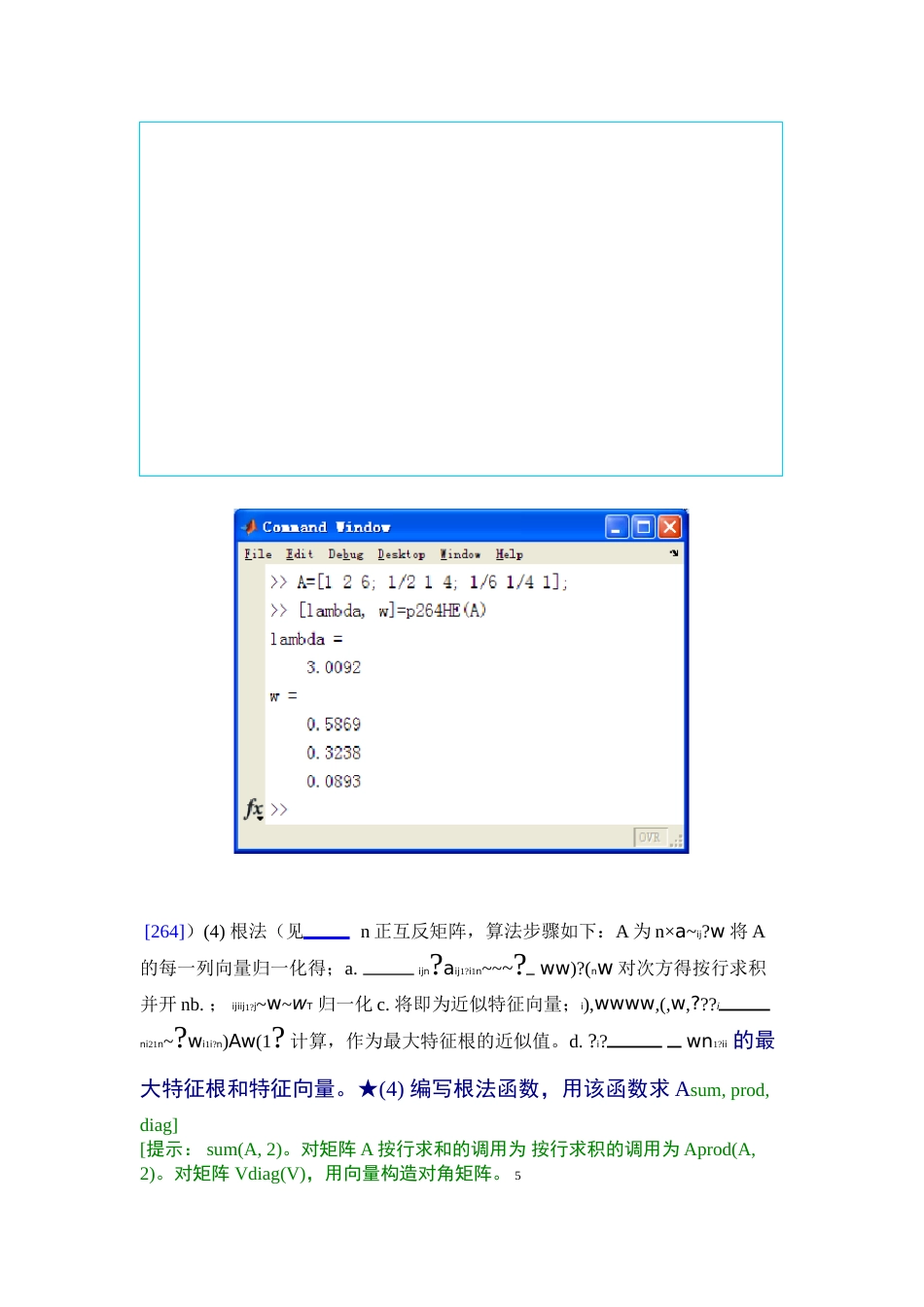
实验09离散模型（2学时）（第8章离散模型）1.层次分析模型1.1（验证，编程）正互反阵最大特征根和特征向量的实用算法p263~264已知正互反阵261????1/21A?4????1/461/1??注：[263]定理2n阶正互反阵A的最大特征根≥n。★(1)用MATLAB函数求A的最大特征根和特征向量。调用及运行结果（见[264]）：>>A=[126;1/214;1/61/41];>>[V,D]=eig(A)V=0.8685-0.8685-0.86850.47790.2390-0.4139i0.2390+0.4139i0.13150.0658+0.1139i0.0658-0.1139iD=3.0092000-0.0046+0.1663i000-0.0046-0.1663i>>D=diag(D)D=3.0092-0.0046+0.1663i-0.0046-0.1663i>>D=D.*(imag(D)==0)D=3.009200>>[lambda,k]=max(D)lambda=13.0092k=1>>w=V(:,k)/sum(V(:,k))w=0.58760.32340.0890[263]）(2)幂法（见n正互反矩阵，算法步骤如下：A为n×(0)w1）；a.任取n维非负归一化初始列向量（分量之和为)k?1)((k2,0,1,?Aww,k?；计算b.1)?(kw1)k?(?w1)k?(w归一化，即令c.；n?1)?(kwi1i?)(1)k(k?1)k?(?)n|?|w,(i?w?1,2,w即，当d.对于预先给定的精度ε时，iib；为所求的特征向量；否则返回到步骤1)?(knw1??i?。e.计算最大特征根)(kwn1i?i注：)k(k?1)(((k)k)???wAw??ww?1)(k?w?in,i?1,2,??)k(wi文件如下：函数式m[lambdaw]=p263MI(A,d)function——求正互反阵最大特征根和特征向量%幂法%A正互反方阵%d精度2%lambda最大特征根归一化特征列向量%w0.000001，则d取if(nargin==1)%若只输入一个变量（即A）d=1e-6;end的阶数取方阵An=length(A);%任取归一化初始列向量w0=w0/sum(w0);%w0=rand(n,1);1whileww=A*w0;%归一化w=ww/sum(ww);all(abs(w-w0)<d)if;breakendw0=w;endlambda=sum(ww./w0)/n;的最大特征根和特征向量。用幂法函数求A☆(2)：）调用及运行结果（[264]）和法（见(3)[264]3A为n×n正互反矩阵，算法步骤如下：a~ijw?a.将A的每一列向量归一化得；ijn?aiji?1n~~~?w?wwb.对；按行求和得iijij1j?~w~Ti)ww,,ww,w(,???w即为近似特征向量；归一化c.将n2i1ni~?wi1?in(Aw)1??i?，作为最大特征根的近似值。d.计算nw1?ii函数式m文件如下：function[lambdaw]=p264HE(A)%和法——求正互反阵最大特征根和特征向量%A正互反方阵%lambda最大特征%w归一化特征列向AA=A/diag(sum(A));%a.的每一列向量归一ww=sum(AA,2);%b.A按行求和w为列向w=ww./sum(ww);%c.归一化，为近似特征列向lambda=sum(A*w./w)/length(A)%d.计算最大特征根的近似☆(3)用和法函数求A的最大特征根和特征向量。调用及运行结果（[264]）：4[264]）(4)根法（见n正互反矩阵，算法步骤如下：A为n×a~ij?w将A的每一列向量归一化得；a.ijn?aij1?i1n~~~?ww)?(nw对次方得按行求积并开nb.；ijiij1?j~w~wT归一化c.将即为近似特征向量；i),wwww,(,w,???ini21n~?wi1i?n)Aw(1?计算，作为最大特征根的近似值。d.?i?wn1?ii的最大特征根和特征向量。★(4)编写根法函数，用该函数求Asum,prod,diag][提示：sum(A,2)。对矩阵A按行求和的调用为按行求积的调用为Aprod(A,2)。对矩阵Vdiag(V)，用向量构造对角矩阵。5nargin，存放函数输入自变量的数目。编写的程序和调用及运行结果（见[264]）：function[lambdaw]=p264GEN(A)%根法——求正互反阵最大特征根和特征向量%A正互反方阵%lambda最大特征根%w归一化特征列向量n=length(A);AA=A/diag(sum(A));%a.将A的每一列向量归一化ww=(prod(AA,2)).^(1/n);%b.对AA按行求积并开n次方，ww为列向量w=ww./sum(ww);%c.归一化，得w为近似特征列向量lambda=sum(A*w./w)/n;%d.计算最大特征根的近似值λ1.2（验证，编程）旅游决策问题p250~256在下面程序中，脚本式m文件p250.m调用函数式m文件p250fun.m（求A的最大特征根及归一化特征列向量、一致性指标值CI、一致性比率值CR），6p250fun.m中调用另一个函数式m文件p264HE.m（求A的最大特征根及归一化特征列向量）。(1)脚本式m文件如下：%旅游决策问题%文件名：p250.mclear;clc;formatcompact;%层次分析法的基本步骤：%1.建立层次结构模型%见p250图1选择旅游地的层次结构%2.构造成对比较阵%第2层为准则层：景色、费用、居住、饮食和旅途5个准则A=[11/2433;...21755;...1/41/711/21/3;...1/31/5211;1/31/5311];%第3层为方案...