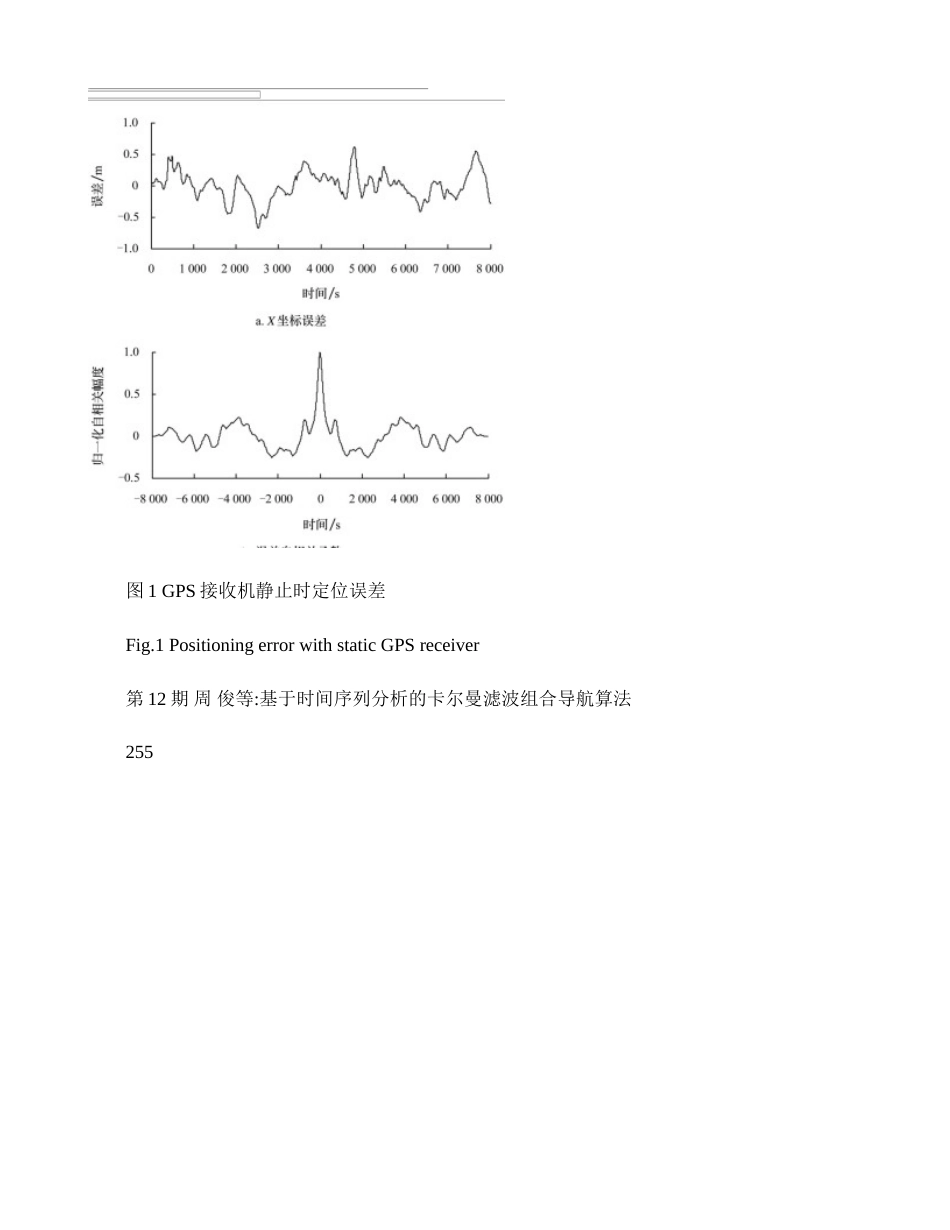
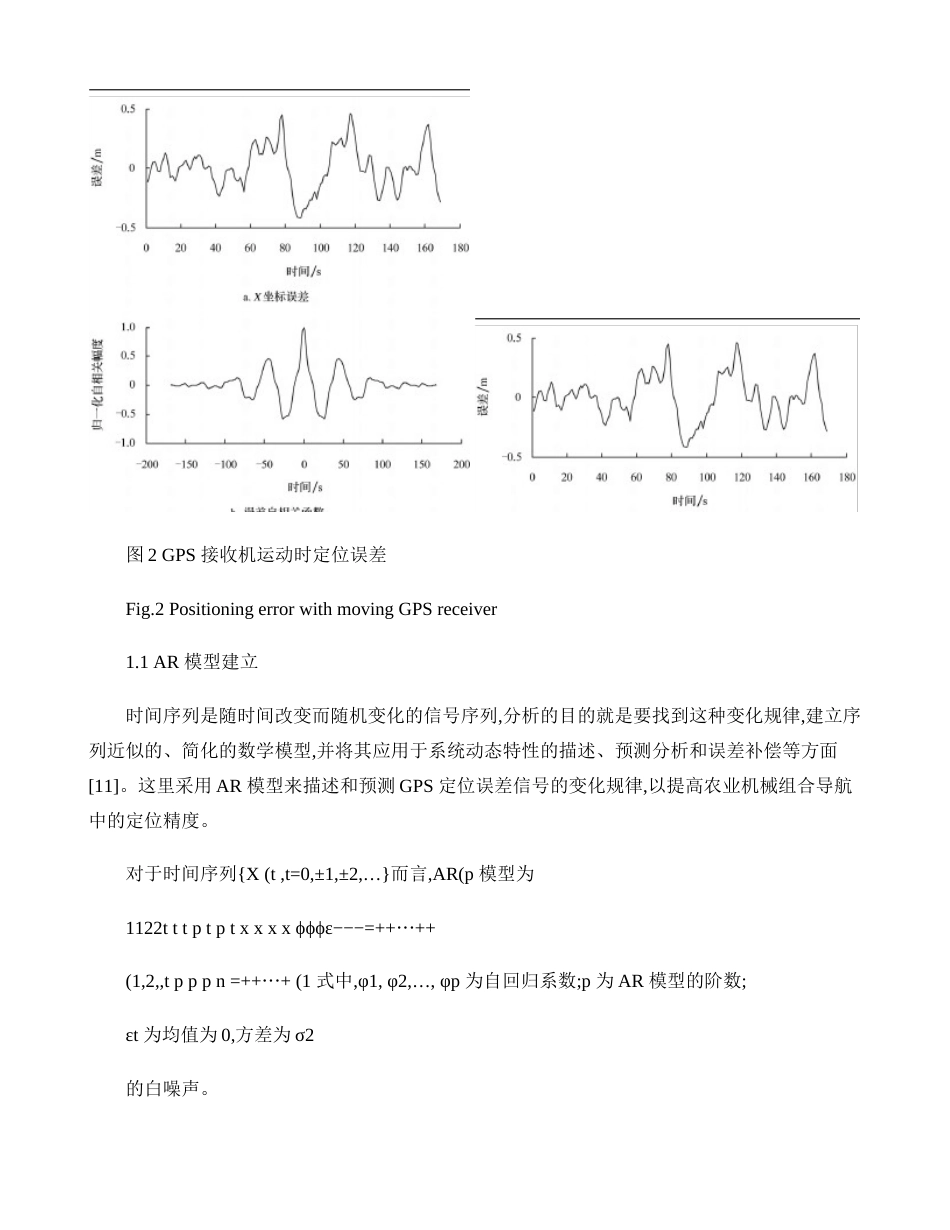
第26卷第12期农业工程学报Vol.26No.122542010年12月TransactionsoftheCSAEDec.2010基于时间序列分析的卡尔曼滤波组合导航算法周俊1,张鹏1,刘成良2(1.南京农业大学工学院,南京210031;2.上海交通大学机械与动力工程学院,上海200240摘要:GPS广泛用于农业机械导航研究中,其定位误差信号一般存在明显的自相关性,不能满足组合导航中常用的卡尔曼滤波算法观测噪声为高斯白噪声的要求。为此,建立了GPS定位误差AR模型,结合卡尔曼估计结果来预测和修正GPS定位误差,再将修正后的GPS定位信息应用于组合导航中的卡尔曼滤波过程。试验结果表明,无论GPS接收机是在静止还是在运动条件下,处理后的定位误差信号自相关性都明显降低,近似为白噪声;目标路径直线时的最大跟踪误差约为0.15m,为曲线时,最大跟踪误差约为0.3m。该方法为低精度GPS应用于农业机械导航提供了可行途径。关键词:农业机器人,导航,全球定位系统,自回归模型,卡尔曼滤波doi:10.3969/j.issn.1002-6819.2010.12.043:TP242文献标志码:A:1002-6819(2010-12-0254-05周俊,张鹏,刘成良.基于时间序列分析的卡尔曼滤波组合导航算法[J].农业工程学报,2010,26(12:254-258.ZhouJun,ZhangPeng,LiuChengliang.Kalmanfilteringforintegratednavigationbasedontimeseriesanalysis[J].TransactionsoftheCSAE,2010,26(12:254-258.(inChinesewithEnglishabstract0引言目前农业机械自主导航中使用GPS绝对定位信息比较普遍[1-3]。为了提高导航系统的精度和可靠性,降低成本,一般还需要在Kalman滤波基础上融合其他传感器信息构成某种组合导航形式[4-9]。如果运动载体的运动状态能用线性模型描述且模型误差和传感器测量误差能用高斯白噪声模型化,则Kalman滤波将在统计意义上提供融合数据的最优估计;反之,则不能。实际应用中,系统噪声和观测噪声往往是有色噪声,因此造成了Kalman滤波效果的下降和较大的系统实际误差产生[10]。GPS定位误差就是一个具有自相关性的有色噪声。本文将采用时间序列分析方法,对农业机械导航过程中的GPS定位误差进行建模,确定GPS定位误差AR模型参数,消除GPS定位误差信号的内在自相关性,使得GPS定位误差信号接近于白噪声。然后以处理后的GPS定位信息为基础,根据Kalman滤波原理建立农业机械组合导航框架,来提高其自主导航系统性能。1GPS定位误差时间序列分析GPS接收机输出的定位信号在时间上是离散的,信号中存在加性噪声,并随着时间随机变化,当前时刻定位误差信号与该时刻之前的误差信号并不完全独立。可以通过大量的观测数据来分析定位误差特性,建立GPS收稿日期:2010-02-25修订日期:2010-08-16基金项目:“国家863”高技术研究发展计划资助项目(2006AA10Z259,2006AA10A304作者简介:周俊(1974—,男,副教授,博士,研究方向:农业机器人、机器视觉与模式识别。南京南京农业大学工学院,210031。Email:zhoujun@njau.edu定位误差模型,以进行误差预测和修正。采用Trimble公司的AgGPS132接收机,连续采集GPS接收机静止和运动时的定位数据,高斯投影后转换为平面直角坐标系下的位置数据(x,y。图1a是接收机静止时X坐标方向的连续8000个采样点构成的误差序列(Y坐标方向有类似的结果,下文同样情况时不再赘述,图1b是对应的定位误差自相关函数曲线。图2a是接收机运动时X坐标的误差序列,图2b是对应的误差自相关函数曲线。可以看出无论是静态还是动态条件下,定位误差序列均具有明显的自相关性。图1GPS接收机静止时定位误差Fig.1PositioningerrorwithstaticGPSreceiver第12期周俊等:基于时间序列分析的卡尔曼滤波组合导航算法255图2GPS接收机运动时定位误差Fig.2PositioningerrorwithmovingGPSreceiver1.1AR模型建立时间序列是随时间改变而随机变化的信号序列,分析的目的就是要找到这种变化规律,建立序列近似的、简化的数学模型,并将其应用于系统动态特性的描述、预测分析和误差补偿等方面[11]。这里采用AR模型来描述和预测GPS定位误差信号的变化规律,以提高农业机械组合导航中的定位精度。对于时间序列{X(t,t=0,±1,±2,…}而言,AR(p模型为1122tttptptxxxxϕϕϕε−−−=++++⋅⋅⋅(1,2,,tpppn=++⋅⋅⋅+(1式中,φ1,φ2,…,φp为自回归系数;p为AR模型的阶数;ε...