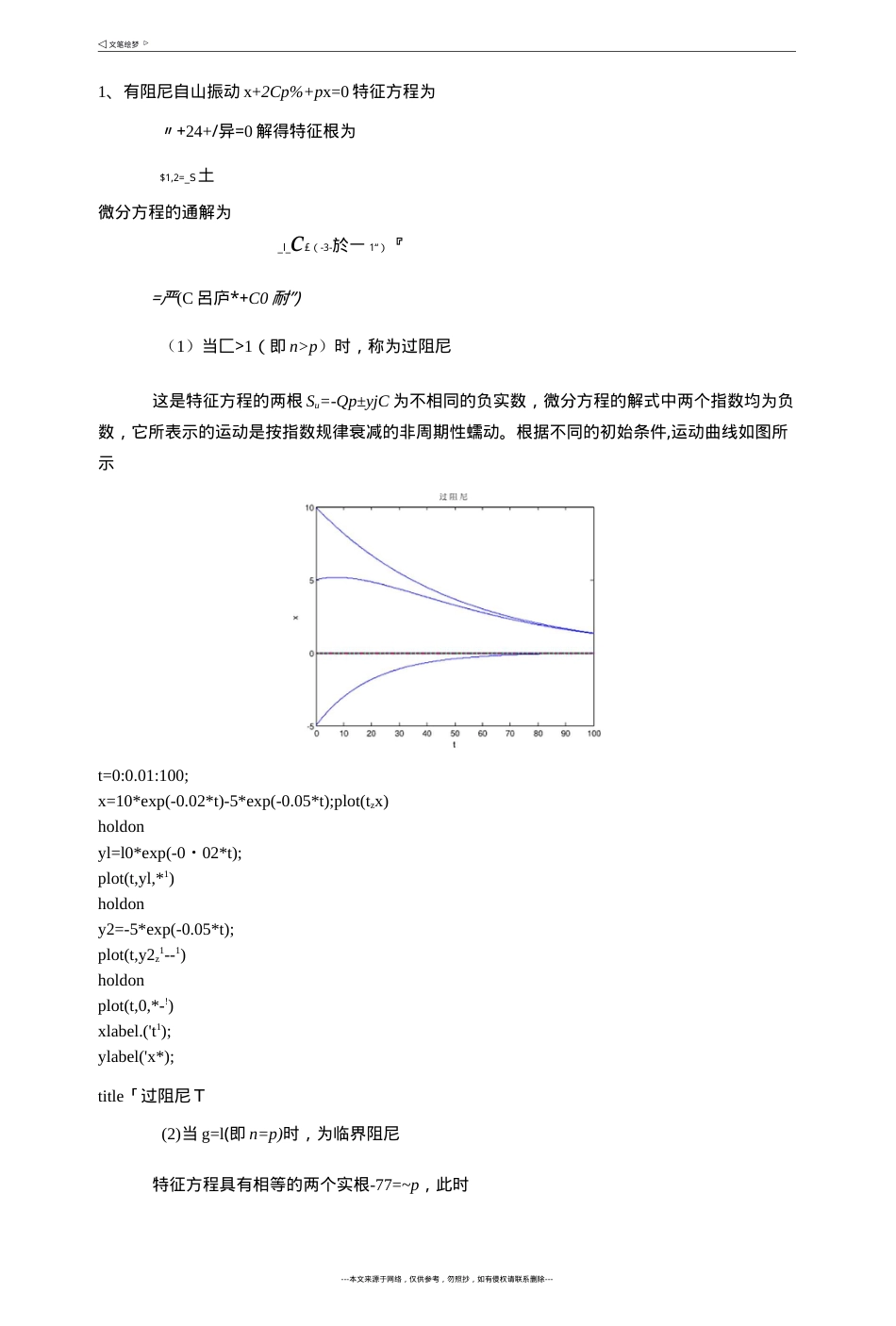
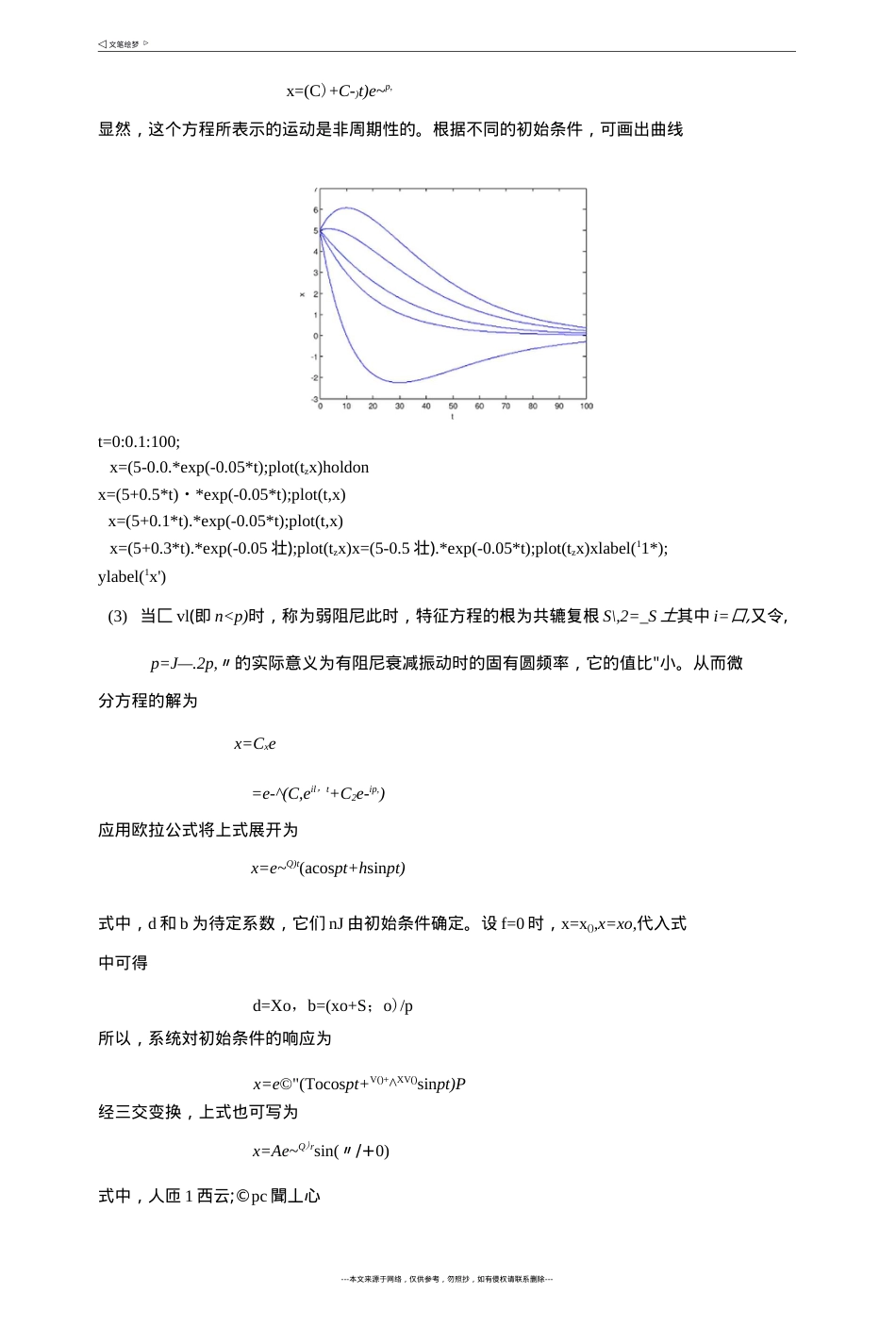
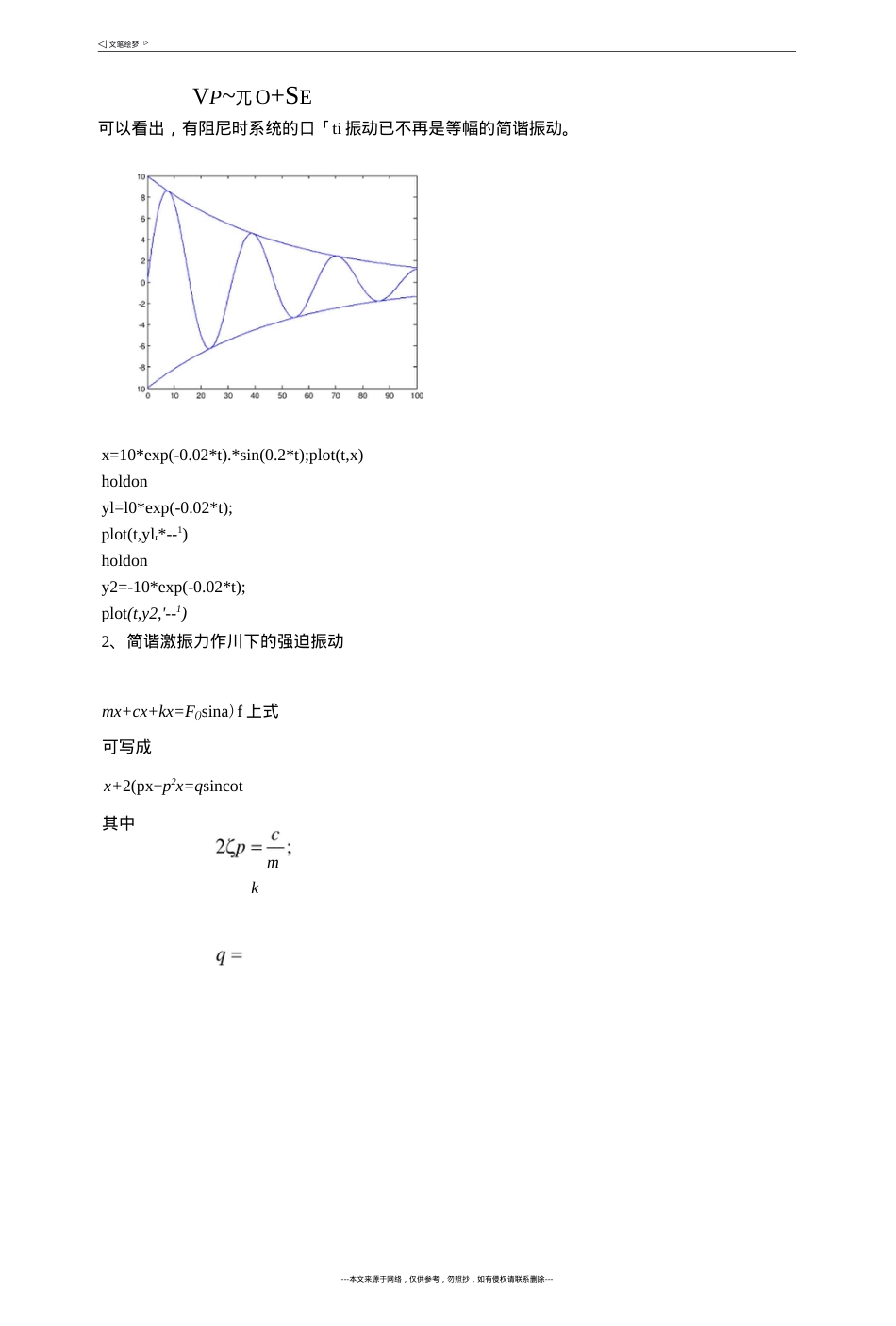
1、有阻尼自山振动x+2Cp%+px=0特征方程为〃+24+/异=0解得特征根为$1,2=_S土微分方程的通解为_l_c£（-3-於一1“）『=严(C呂庐*+C0耐”)（1）当匚>1（即n>p）时，称为过阻尼这是特征方程的两根Su=-Qp±yjC为不相同的负实数，微分方程的解式中两个指数均为负数，它所表示的运动是按指数规律衰减的非周期性蠕动。根据不同的初始条件,运动曲线如图所示t=0:0.01:100;x=10*exp(-0.02*t)-5*exp(-0.05*t);plot(tzx)holdonyl=l0*exp(-0・02*t);plot(t,yl,*1)holdony2=-5*exp(-0.05*t);plot(t,y2z1--1)holdonplot(t,0,*-!)xlabel.('t1);ylabel('x*);title「过阻尼T(2)当g=l(即n=p)时，为临界阻尼特征方程具有相等的两个实根-77=~p，此时---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---x=(C)+C-)t)e~p,显然，这个方程所表示的运动是非周期性的。根据不同的初始条件，可画出曲线t=0:0.1:100;x=(5-0.0.*exp(-0.05*t);plot(tzx)holdonx=(5+0.5*t)・*exp(-0.05*t);plot(t,x)x=(5+0.1*t).*exp(-0.05*t);plot(t,x)x=(5+0.3*t).*exp(-0.05壮);plot(tzx)x=(5-0.5壮).*exp(-0.05*t);plot(tzx)xlabel(11*);ylabel(1x')(3)当匚vl(即n<p)时，称为弱阻尼此时，特征方程的根为共辘复根S\,2=_S土其中i=口,又令,p=J—.2p,〃的实际意义为有阻尼衰减振动时的固有圆频率，它的值比"小。从而微分方程的解为x=Cxe=e-^(C,eil，t+C2e-ip,)应用欧拉公式将上式展开为x=e~Q)t(acospt+hsinpt)式中，d和b为待定系数，它们nJ由初始条件确定。设f=0时，x=x(),x=xo,代入式中可得d=Xo，b=(xo+S；o)/p所以，系统対初始条件的响应为x=e©"(Tocospt+V()+^XV()sinpt)P经三交变换，上式也可写为x=Ae~Q)rsin(〃/+0)式中，人匝1西云;©pc聞丄心---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---VP~兀O+SE可以看出，有阻尼时系统的口「ti振动已不再是等幅的简谐振动。---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---x=10*exp(-0.02*t).*sin(0.2*t);plot(t,x)holdonyl=l0*exp(-0.02*t);plot(t,ylr*--1)holdony2=-10*exp(-0.02*t);plot(t,y2,'--1)2、简谐激振力作川下的强迫振动mx+cx+kx=F()sina)f上式可写成x+2(px+p2x=qsincot其中mkx=x}+x2西对应于有阻尼自由振动齐次方程的解，在弱阻尼匚＜1的情况卜・,X］=Ae~^sin（pt+0）为瞬态振动特解兀2代表系统在简谐激振下产生的强迫振动，为稳态振动。x2=Xsin（cot-中）式中X——振动相应的幅值co激振力圆频率中相应滞后于激励的相位差又有X2=（0%COS（3/—中）aX2=-coXsin（ojZ-中）将上述三式代入微分方程得-co2Xsin（cof—中）+2Q;coXcos（a）/—中）+p2Xsin（cor-中）u/sinco/乂利川三介关系qsinco/=qsin［（co/一中）+中］二qcos中sin（co/-中）+qsin中cos（co/一中）比较得，sin（co/-中）和cos（a）f-中）前的系数必须两两相等，即（p2-co2）X=geos中---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---rh此解得X。7（l-V）2+（2^）2---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---2«-）p中=arctani-A2p式中x——频率比P---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---2Ck=arctan7l-VqF0/m=F._系统的最大静位移。p2k/mk所以，求得强迫振动的稳态解为X二/°=sin(cof-中)■J(1—F)2+(2S)2在简谐激振力作用下，强迫振动也为简谐振动，其频率与激振频率3相同，但相位滞后中，这是由于阻尼存在的关系。取X与X。之比为p_x1XoJ(l-F)2+(2S)2p称为放大因子，它代表稳态振幅X与激振力幅吒静止作川于弹簧上的静位移X°Z比。0值不仅随入而变，而且还随匚值而变。在不同©值时,放大因子卩与频率比九的关系以及相位角中的关系如图所示(1)当X«l,即激振频率co远小丁•系统的固有频率P时，无论阻尼大小如何，B接近于1,即振幅近似等于激振力幅值吒作用下的静变形X。。(2)当九＞〉1,即激振频率C0远大于系统的固有频率P时，卩趋近于0.(3)当九U1,即3接近于P，振幅X急剧增加，卩趋向于pmax,这种现象称为共振。幅频待性柿频特性S二［0.10.15...